
Einleitung
Kundenindividuelle Massenproduktion, demografischer Wandel, Arbeitskräftemangel und Verlagerung von Produktionsstätten sind einige der globalen Herausforderungen, mit denen produzierende Unternehmen weltweit konfrontiert werden. Folglich verlangen Produktionsstandorte in Hochlohnländern nach hochautomatisierten und flexiblen Produktionssystemen, um wettbewerbsfähig zu bleiben. Industrieroboter und Sondermaschinen haben sich bei der Bewältigung einiger dieser Herausforderungen als wichtige Hilfsmittel und Wegbereiter erwiesen. Die flexible Programmierung solcher Fertigungssysteme ermöglicht es, Aufgaben wie Handhabung, Transport und verschiedene Produktionsprozesse automatisch mit hoher Präzision, Geschwindigkeit und Qualität durchzuführen.
Zwar wurden die Vorteile solcher Produktionssysteme vielfach nachgewiesen, es ist jedoch zu beachten, dass ein erheblicher Integrations- und Programmieraufwand erforderlich ist, bevor diese Systeme produktiv eingesetzt werden können. In den meisten Fällen erfordert die Softwareentwicklung für Produktionssysteme den Einsatz physischer Komponenten unter realen Bedingungen. Die Verfügbarkeit solcher Systeme ist jedoch häufig aus verschiedenen Gründen eingeschränkt, beispielsweise weil das System in Betrieb ist, parallel entwickelt wird oder im schlechtesten Falle überhaupt nicht existiert. Dieses Problem führt dazu, dass die Entwicklung der Software verzögert oder aufgeschoben wird, bis die erforderlichen physischen Komponenten verfügbar und integriert sind. Zudem gilt die Programmierung eines Industrieroboters als eine nicht gerade triviale Aufgabe, die qualifizierte Bedienende mit einem guten räumlichen Verständnis des Arbeitsbereichs und mit Fachkompetenz erfordert. Die Herausforderung besteht darin, eine Bewegungssequenz zu programmieren, die den Ablauf des Produktionsprozesses und die Prozessqualität sicherstellt und gleichzeitig Kollisionen vermeidet. Deshalb wird die Programmierung von Industrierobotern heutzutage häufig noch manuell durchgeführt und gilt als eine anspruchsvolle und ressourcenintensive Aufgabe.
Die Probleme der Roboterprogrammierung sind auf einer abstrakteren Ebene auch bei der Softwareentwicklung in anderen Bereichen anzutreffen. Es stellt sich also folgende Frage: Wie gehen Softwareentwickler mit diesen Problemen um, wenn es zum Beispiel keine Module oder Schnittstellen gibt? Die Antwort: Wir erstellen Mock-ups! In gewisser Weise sind Mock-ups nichts anderes als Modelle, die eine gewünschte Funktion simulieren. Allerdings klingt die Modellierung eines Roboters ein wenig komplizierter als die Implementation einer Datenbank oder einer Schnittstelle. Dieser Blogartikel soll das Gegenteil beweisen und zeigt in einem kurzen Tutorial, wie man kinematische Simulationsmodelle einfach und effizient erstellen kann, um die Programmierung solcher Fertigungssysteme zu erleichtern.
Dieser Blogbeitrag soll den Lesern Folgendes vermitteln:
- Grundlegendes Verständnis von kinematischen Simulationsmodellen
- Die Möglichkeit, ein einfaches kinematisches Modell eines Manipulators (z. B. Roboter, Drehtisch, Linearachsen) basierend auf freier und Open-Source-Software (FOSS) zu erstellen, das für Prototyping-, Entwicklungs- und Testzwecke verwendet werden kann
Kinematische Modellierung
Bezugssystem
Im Vorfeld der Simulation der Kinematik eines Robotersystems müssen zunächst einige grundlegende mathematische Konzepte und die im Zusammenhang mit der kinematischen Modellierung genutzte Terminologie verstanden werden. Zu diesem Zweck betrachten wir zunächst ein minimales System, das aus einem Drehgelenk \(j_1\) und eine Achse \(l_1\) besteht.
Die Achse ist starr mit dem Gelenk verbunden. Das bedeutet, wenn das Gelenk um seine z-Achse (Frame \(B_{j_1}\)) um einen Winkel von \(\phi_{j_1}\) rotiert, dreht sich die Achse \(l_1\) mit. Gehen wir hier davon aus, dass sich der Ursprungskoordinatenframe des Systems im Basiskoordinatenframe bei \(B_0\) befindet. Darüber hinaus beschreibt der Vektor \(p_0^w := (x, y, z, a^x, \beta^y, \phi^z)^T\) die Pose (Position und Rotation) der Achse im Arbeitsframe \(B_w\). Das kinematische 2D-Modell eines solchen Systems und seiner Komponenten ist links in Abbildung 1 dargestellt.
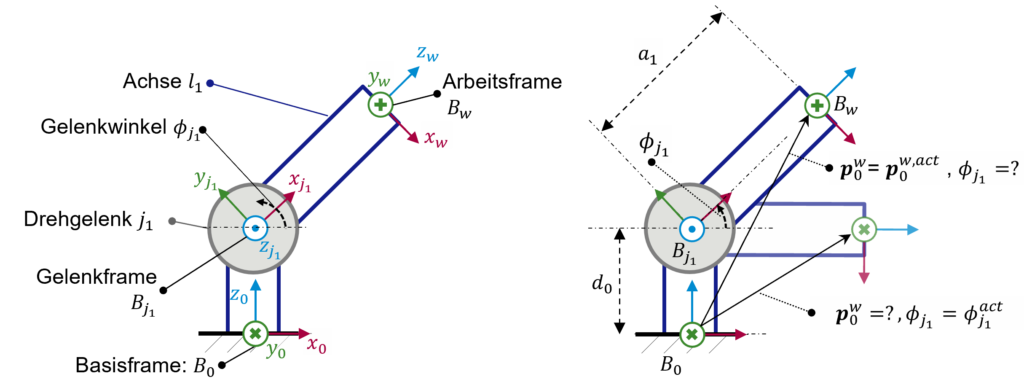
Kinematisches Modell
Wenn wir davon ausgehen, dass wir einige Bewegungen programmieren oder simulieren müssen, werden wir zwangsläufig mit mindestens einem der folgenden Probleme konfrontiert:
- Inverskinematik-Problem: Welcher Winkel \(\phi_{j1}\) entspricht einer aktuellen Pose \(p_0^{w,act}\)?
- Vorwärtskinematik-Problem: Welches ist die resultierende Pose \(p_0^w\) für einen gegebenen Gelenkwinkel \(\phi_{j1}^{act}\)?
Diese Fragen werden auf der rechten Seite von Abbildung 1 visualisiert und stellen die grundlegenden Probleme der kinematischen Modellierung dar, die als Inverskinematik- und Vorwärtskinematik-Probleme bezeichnet werden. Um diese Fragen zu beantworten, müssen zunächst alle räumlichen Beziehungen zwischen allen aufeinanderfolgenden[1] Frames des Systems abgeschätzt werden. Das heißt von der Basis \(B_0\) zum Gelenk \(B_{j1}\) und vom Gelenk \(B_{j1}\) zum Arbeitsframe \(B_w\). Die relativen räumlichen Beziehungen[2] zwischen zwei Frames werden durch die Translationskomponenten \(x_{\Delta}, y_{\Delta}\), und
| Base Frame | Reference Frame | Translation | Rotation |
|---|---|---|---|
| Basis \(B_0\) | Gelenk \(B_{j_1}\) | \(x_{\Delta}\) = 0, \(y_{\Delta}\) = 0, \(z_{\Delta}\) = \(d_0\) | \(\alpha_{\Delta}^x\) = 0, \(\beta_{\Delta}^y\) = 0, \(\phi_{\Delta}^z\) = \(\phi_{j_1}\) |
| Gelenk \(B_{j_1}\) | Arbeitsframe \(B_w\) | \(x_{\Delta}\) = \(a_1\), \(y_{\Delta}\) = 0, \(z_{\Delta}\) = \(d_0\) | \(\alpha_{\Delta}^x\) = -90°, \(\beta_{\Delta}^y\) = 0, \(\phi_{\Delta}^z\) = 0 |
Nachdem wir nun die geometrischen Beziehungen unseres Systems definiert haben, kann das kinematische Modell, mithilfe dessen die vorhergehenden Fragen beantwortet werden, beschrieben werden. Das Vorwärtskinematik-Model, dass die resultierende Pose für einen angeordneten Gelenkwinkel liefert, könnte beispielsweise mithilfe der in Abbildung 2 dargestellten trigonometrischen Beziehungen abgebildet werden.
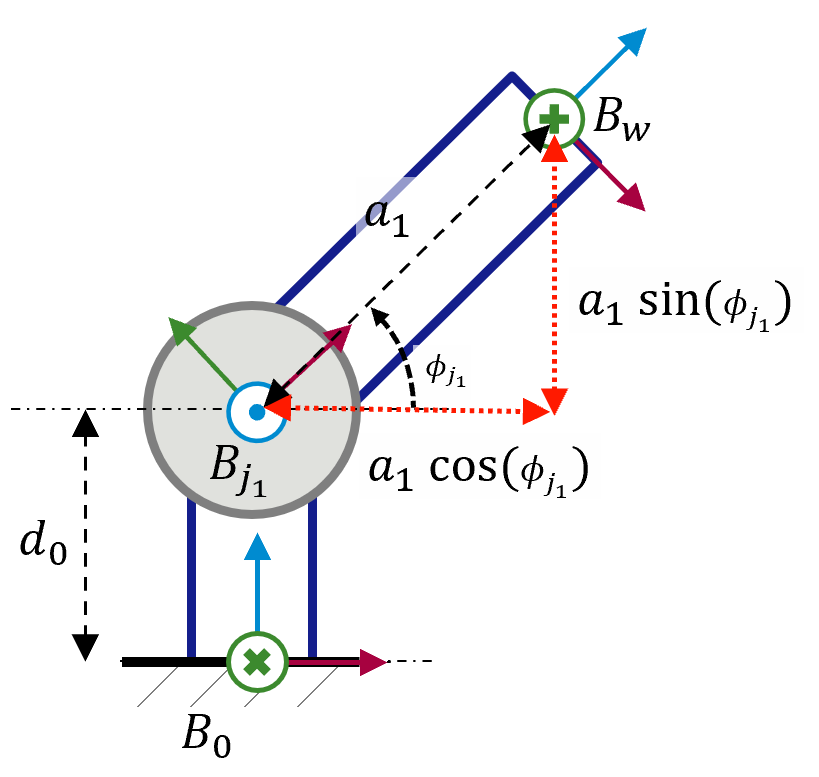
Obwohl diese geometrischen Funktionen die Kinematik unseres Bezugssystems ausreichend modellieren, ist hierbei zu beachten, dass die Beschreibung des kinematischen Modells auf diese Weise für komplexere Systeme mit mehreren Gelenken und Achsen nicht so einfach ist. Aus diesem Grund werden zur Berechnung von Mehrkoordinatentransformationen in der Regel andere mathematische Ansätze genutzt, z. B. homogene Matrizen oder Quaternionen. Die Beschreibung dieser Methoden würde den Rahmen dieses Blogbeitrags sprengen. Für den Rest des Artikels ist es ausreichend zu wissen, welche Eingaben und Ausgaben wir von einem kinematischen Modell erwarten können. Diese Modelle können als Black-Box-Komponenten angenommen werden, wie in Abbildung 3 dargestellt.
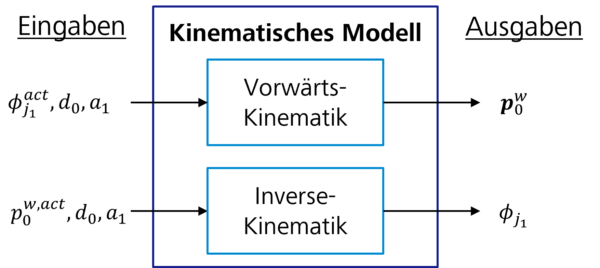
Implementierung
Nach der Einführung der zentralen Konzepte der kinematischen Modellierung wird eine einfache Möglichkeit zur Implementierung kinematischer Ketten vorgestellt.
In der Industrie gibt es bereits eine Reihe von Spezifikationen und Formaten, die sich mit der Modellierung von kinematischen Ketten befassen, z. B. Collada, AutomationML, OPC UA Robotics. Unserer Erfahrung nach hat sich jedoch kein branchenweites Standardformat durchgesetzt. Dies stellt ein umfassenderes Problem auf dem Gebiet der Robotik dar, wo Programmiersprachen hauptsächlich herstellerspezifisch sind und es keine Standards für die Roboterprogrammierung oder -modellierung gibt. Dies ist einer der Gründe, weshalb das Robot Operating System (ROS) im Jahr 2010 ins Leben gerufen wurde. ROS ist eine FOSS-Robotik-Middleware, die verschiedene Bibliotheken (z. B. kinematische Modellierung, Wahrnehmung, Visualisierung, Bahnplanung) für die hardwareunabhängige Programmierung von Robotersystemen enthält. Diese Eigenschaften haben ROS zu einem Framework gemacht, das in der Robotikforschung als Stand der Technik gilt. Aufgrund der Beliebtheit und der Merkmale des ROS-Frameworks (z. B. Leistungsfähigkeit, Hardwareneutralität, FOSS, Modularität, Skalierbarkeit) haben Hersteller von Robotern und Feldgeräten (z. B. Greifer und Sensoren) sowie Drittanbieter von Software begonnen, Programmierschnittstellen für ROS anzubieten.
Im Rahmen der Entwicklung von ROS wurde das Unified Robot Description Format (URDF) zur Modellierung von kinematischen Ketten eingeführt. Beim URDF handelt es sich um ein offenes Standard-XML-Schema zur Beschreibung der geometrischen Beziehungen zwischen Gelenken und Achsen eines Roboters. Zusätzlich zur Modellierung kinematischer Ketten bietet das URDF die Möglichkeit, die physikalischen Eigenschaften von Gelenken zu modellieren (z. B. Trägheit, Dynamik und Achsenbegrenzungen) oder CAD-Dateien zur Modellierung der Volumeneigenschaften von Achsen zu verwenden, die für Kollisionstests genutzt werden können. Da das URDF einem XML-Schema folgt, können kinematische Modelle darüber hinaus einfach und lesbar dargestellt werden. So beschreibt der folgende Auszug in Abbildung 4 beispielsweise die kinematischen Beziehungen zwischen dem Gelenk j1 und der Achse l1 aus Tabelle 1.
Nachdem die geometrischen Beziehungen zwischen allen Achsen und Gelenken mithilfe einer URDF-Datei beschrieben wurden, kann das kinematische Modell visualisiert und zur Berechnung von Endeffektorpositionen oder erforderlichen Gelenkrotationen genutzt werden. ROS enthält eine Handvoll Pakete basierend auf Bibliotheken von Drittanbietern, die alle diese Funktionen implementieren. Die Verwendung dieser Bibliotheken ist in der ROS-Dokumentation beschrieben.
<!--Alle Achsen unseres Modells.--> <!--Das Root-Frame in ROS wird base_link genannt und repräsentiert das Root-Frame (B_0) in unserem System. --> <link name="base_link"/> <!--Achse 1 unseres Modells. --> <link name="link_1"/> <!-- Der Arbeitsframe unseres Modells wird als Achse dargestellt.--> <link name="work_frame"/> <!--Alle Gelenke unseres Modells.--> <!--Das Drehgelenk 1, das die Basisachse (parent-Achse) mit Achse 1 (child-Achse) verbindet, wird hier modelliert. Das Gelenk befindet sich im Ursprung der child-Achse.--> <joint name="joint_1" type="revolute"> <parent link="base_link"/> <child link="link_1"/> <!-- Auswahl der Rotationsachse, in unserem Fall um das Gelenk um die z-Achse in positiver Richtung.--> <axis xyz="0 0 1"/> <!-- Hier wird die Transformation zwischen parent- und child-Achse angegeben.--> <!-- Die Translationskomponenten (xyz) werden in Metern angegeben. --> <!-- Die Rotation wird durch die Euler-Winkel (rpy) in Radianten ausgedrückt, und zwar nach folgender Notation (r)oll (x-Achsen-Rotation), (p)itch (y-Achsen-Rotation) und (y)aw (z-Achsen-Rotation). --> <origin xyz="0 0 0,4" rpy="1,57079632679 0,0 0,0"/> <!-- Das Modell eines beweglichen Gelenks muss weitere physikalische Eigenschaften umfassen. --> <limit effort="100" lower="-0,175" upper="3,1416" velocity="0,5"/> </joint>
Abbildung 4: URDF-Auszug zur Beschreibung der kinematischen Beziehung zwischen Gelenk \(j_1\) und Achse \(l_1\)
Erweitertes System
Nachdem die Grundlagen der kinematischen Modellierung und die Verwendung von URDF zur Implementierung eines kinematischen Modells verstanden wurde, steht der Beschreibung komplexerer kinematischer Ketten mit mehreren Gelenken, wie in Abbildung 5 dargestellt, nichts mehr im Wege.
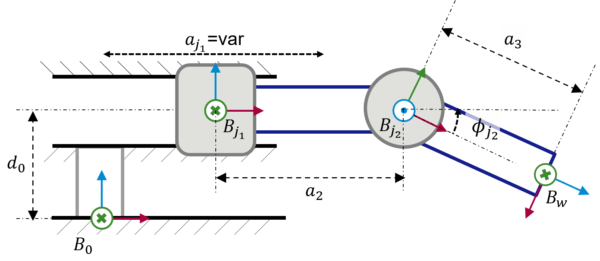
Die entsprechenden geometrischen Beziehungen sind in Tabelle 2 angegeben. Darüber hinaus ist das vollständige URDF im Anhang zu finden.
| Base Frame | Reference Frame | Translation | Rotation |
|---|---|---|---|
| Basis \(B_0\) | Gelenk \(B_{j_1}\) | \(\Delta x\) = \(a_{j_1}\), \(\Delta y\) = 0, \(\Delta z\) = \(d_0\) | \(\alpha_x\) = 0, \(\beta_y\) = 0, \(\phi_z = 0\) |
| Gelenk \(B_{j_1}\) | Gelenk \(B_{j_2}\) | \(\Delta\)x = \(a_2\), \(\Delta y\) = 0, \(\Delta z\) = 0 | \(\alpha_x\) = 90°, \(\beta_y\) = 0, \(\phi_z\) = 0 |
| Gelenk \(B_{j_2}\) | Arbeitsframe \(B_w\) | \(\Delta\)x = \(a_3\), \(\Delta y\) = 0, \(\Delta z\) = 0 | \(\alpha_x\) = -90°, \(\beta_y\) = 0, \(\phi_z\) = 0 |
Das URDF kann anschließend direkt in ROS zur Visualisierung und Positionierung von Gelenken verwendet werden, wie in Abbildung 6 dargestellt.
Gelenk1: \(a_{j_1}\) = -170mm, Gelenk2: \(\phi_{j_2}\) = -48°
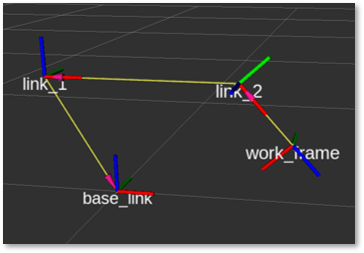
Gelenk1: \(a_{j_1}\) = 80mm, Gelenk2: \(\phi_{j_2}\) = 52°

Abbildung 6: URDF-Visualisierung in ROS mit zwei verschiedenen Gelenkkonfigurationen und folgenden Werten: \(d_0\) = 300mm, \(a_2\) = 500mm, \(a_3\) = 200mm. Die Abbildung rechts zeigt auch die Integration von Oberflächenmodellen zur Modellierung der Volumeneigenschaften der Achsen.
Zusammenfassung und Ausblick
Die Programmierung eines Roboters ist eine komplexe und ressourcenintensive Aufgabe, die in den meisten Fällen auch die Nutzung des physikalischen Systems erfordert. Diese Hindernisse wirken sich direkt auf die Softwareentwicklung und Inbetriebnahme solcher Systeme aus. Ein kinematisches Modell (Mock-up) des Roboters hat das Potenzial, die Programmierung zu vereinfachen, ohne dabei das physische System zu benötigen, und gleichzeitig die Kosten zu senken. Allerdings gilt die Modellierung von Robotersystemen als eine nicht gerade triviale Aufgabe, die in einem ersten Schritt die Beschreibung ihres kinematischen Modells erfordert. Deshalb wurden in diesem Blogbeitrag zunächst die mathematischen Mindestgrundlagen zum Verständnis der kinematischen Modellierung vorgestellt. In einem weiteren Schritt haben wir anschließend gezeigt, wie kinematische Modelle mithilfe des Standardformats URDF nahtlos implementiert werden können.
Mit den Erkenntnissen in diesem Blogbeitrag sollten die Leser in der Lage sein, kinematische Modelle zu beschreiben, die als Mock-ups für Prototyping- oder Entwicklungszwecke eingesetzt werden können. Nachdem nun die erste Hürde der kinematischen Modellierung überwunden ist, können sich die Anwender solche Modelle mit folgenden Themen auseinandersetzen:
- Integration des kinematischen Modells in ein reales Robotersystem und Aufbau eines digitalen Zwillings (weiterführende Literatur: Smart Manufacturing, IoT mit Azure Digital Twins)
- Bereitstellung kinematischer Modelle als Microservices für Entwicklungs-, Test- und Inbetriebnahmezwecke (weiterführende Literatur: Mocks in der Testumgebung)
- Entwicklung anwenderfreundlicherer Programmier-Frameworks basierend auf kinematischen Simulationen unter Einsatz von VR (Virtual Reality) oder AR (Augmented Reality)
Minimales kinematisches Modell (URDF):
Erweitertes kinematisches Modell (URDF):
[1] Aus diesem Grund werden diese Modelle im Allgemeinen als serielle kinematische Ketten bezeichnet. Es gibt auch parallele kinematische Modelle zur Darstellung von Delta-Robotern. Die kinematische Modellierung solcher Systeme wird im Rahmen dieses Blogbeitrags nicht behandelt.
[2] Auf dem Gebiet der Robotik wird die Transformation zwischen zwei Koordinatenframes häufig mit homogenen Transformationen und einer Gruppe von vier Parametern beschrieben, die die Translations- und Orientierungsverschiebung beschreiben. Diese Parameter werden als die Denavit-Hartenberg-Parameter bezeichnet.