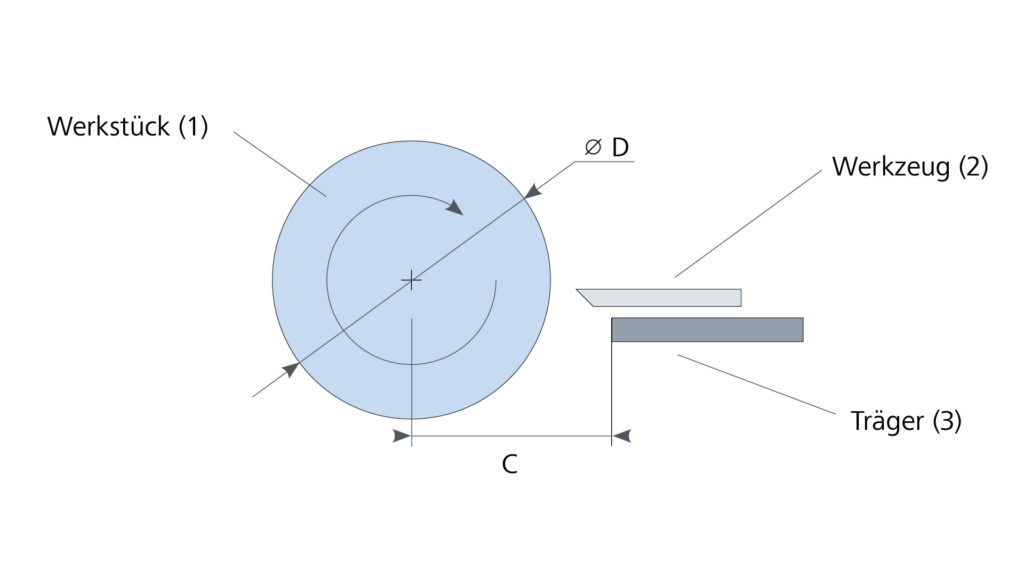
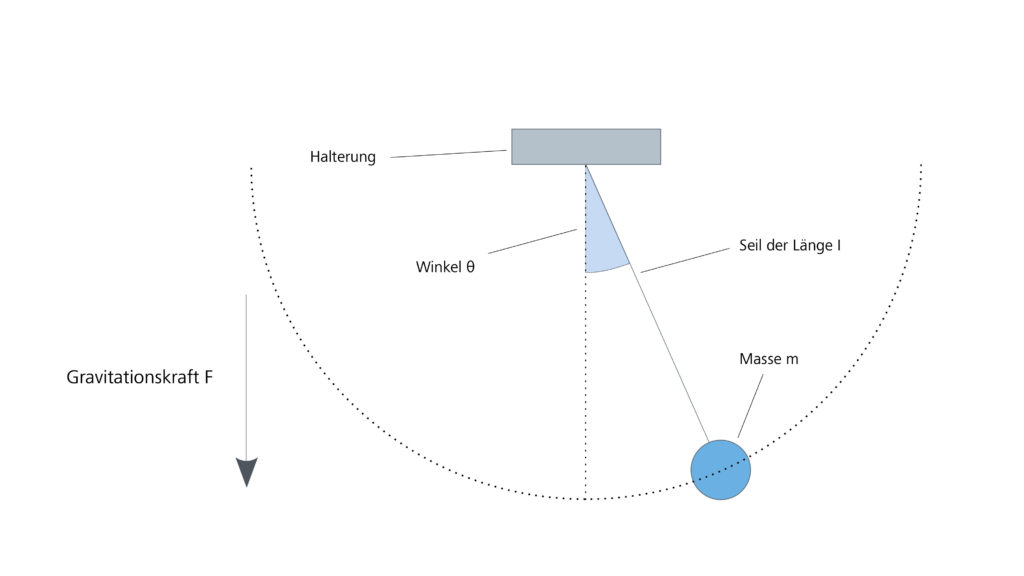
Dieser dritte und letzte Teil der Artikelserie zur datengetriebenen Prozessregelung liefert eine Einführung in Ansätze zur Regelung von Systemen. Im Mittelpunkt steht dabei das klassische „Model-Predictive-Control“ Schema, welches mit den Ergebnissen zur Systemmodellierung aus dem zweiten Artikel zu einer rein datengetriebenen Regelungsstrategie kombiniert wird.

Für die Regelung von Systemen existieren zahlreiche theoretische wie praktische Ansätze. Eine der einfachsten stellen sogenannte PID Regler dar, die in Anwendungen wie Motor- und Temperaturreglungen, Laderegelungen für Solaranlagen oder Reglern für Leistungselektronik zum Einsatz kommen.

Wir wollen uns allerdings mit einer fortgeschritteneren Regelungsstrategie für ein breiteres Anwendungsspektrum befassen, dem „Model Predictive Control (MPC)“ (siehe [3] und [4]). Wie aus der Bezeichnung zu entnehmen ist, setzt diese Strategie die Fähigkeit zur Vorhersage des Systemverhaltens voraus. Eine Anforderung, die durch Modellbildung im Sinne des vorangegangenen Abschnittes aber auch durch den vorgestellten databasierten Ansatz erfüllt werden kann.

Gegenstand der Regelungsstrategie ist die Steuerung der Ausgangszielgrößen durch Modifikation der Eingriffsgrößen, so dass erstere in einem durch Referenzdaten bestimmten Korridor verbleiben.

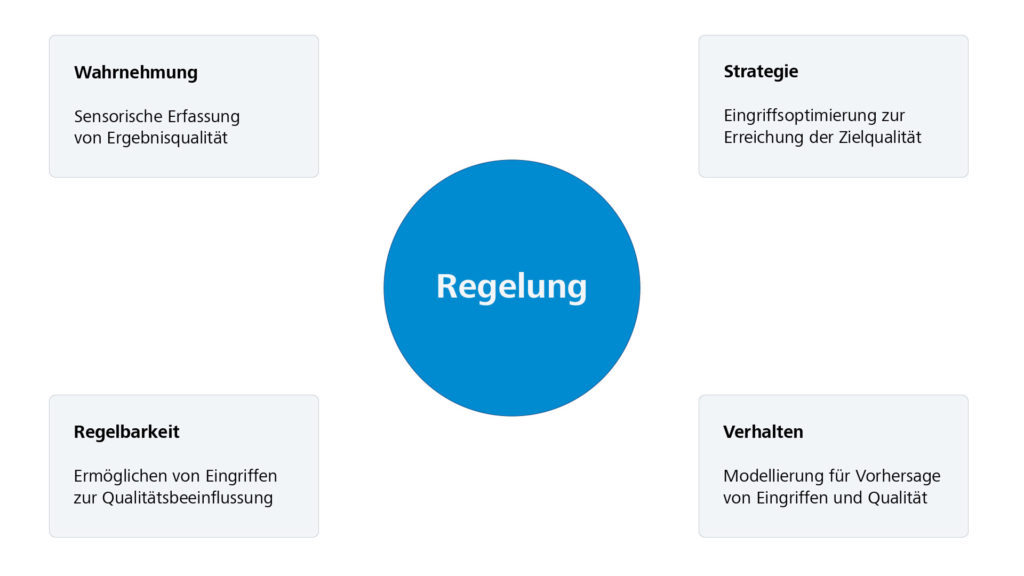
Die MPC Strategie stellt einen iterativen Prozess dar, der aus den drei folgenden Phasen besteht (siehe auch Abbildung 1).

1. Ausgangspunkt bilden historische Daten des zu regelnden Systems. Diese bestehen zum einen aus den Werten der Eingriffsparameter in zurückliegenden Regelschritten und zum anderen aus den zugehörigen, vom System gelieferten Ausgabedaten. Da auch die Referenzdaten sich mit der Zeit verändern können, stellen auch sie einen Teil der historischen Daten dar. Diese Datenbasis repräsentiert also den Status quo des betrachteten Systems. Jede Vorhersage des Systemverhaltens muss sich nahtlos an diese Historie anfügen.
2. Ausgehend vom bestehenden Systemzustand wird das Modell des Systems dazu verwendet, eine optimale Vorhersage von zukünftigen Eingriffsgrößen und zugehörigen Ausgaben zu berechnen. Das entscheidende Optimierungskriterium stellt dabei die Forderung dar, dass sich die Ausgabe des Systems im betrachteten Vorhersagezeitraum bestmöglich den gewünschten Referenzwerten annähert (siehe „Mathematischer Hintergrund“). Dabei gilt es zusätzlich, die technischen Rand- und Grenzbedingungen der Eingriffsparameter zu berücksichtigen.
3. Der dritte und letzte Schritt besteht in der Anwendung der berechneten Eingriffsgrößen im System selbst. Dies entspricht einem Praxistest des zur Vorhersage verwendeten Modells. Darüber hinaus werden die vorhergesagten Eingriffsgrößen nicht über den gesamten festgelegten Vorhersagehorizont angewendet sondern nur für einige wenige Schritte. Dies erfolgt in dem Wissen, dass vom Modell unberücksichtigte Einflüsse das Feedback verfälschen und damit die Genauigkeit der Vorhersagen einschränken. Gleichzeitig sichert das Feedback die Stabilität der Strategie, da die neu gewonnenen Daten in die Datenhistorie eingehen und so die aktualisierte Basis für die nächste Vorhersage bilden.

Diese drei beschriebenen Phasen werden zyklisch durchlaufen. Die Frequenz dieses Prozesses hängt unmittelbar von den Erfordernissen des jeweiligen Anwendungsfalles ab. Insbesondere bei der Regelung von Echtzeitsystemen wie Fahr- und Flugzeugen sind hier Frequenzen von einigen 10Hz notwendig.

Mathematischer Hintergrund

Das „Model Predictive Control“ Schema beinhaltet als zentrales Element die Vorhersage der
zukünftigen Eingabeparameter und Ausgabegrößen , welche den Abstand zu einer Referenztrajektorie
im Vorhersagezeithoriziont minimieren. Zusätzlich sind historische Daten in Form einer Anfangstrajektorie der Länge gegeben, welche durch die gesuchte Trajektorie fortzusetzen ist.

Da die algebraische Repräsentation des zeitbeschränkten Verhaltens es erlaubt, für jedes einen Vektor zu bestimmen, für den gilt, können wir folgendes restringierte Optimierungsproblem für aufstellen

   

unter Verwendung der Zerlegung

   

Die Nebenbedingung sichert dabei die Einhaltung der Anfangsbedingung und die Verwendung von im Minimierungfunktional erzwingt, dass die ermittelte zukünftige Trajektorie zulässig ist für das System . Zusätzlich können Nebenbedingungen an formuliert werden, was aus Gründen der Übersichtlichkeit hier nicht erfolgte. Weitere Details sind in [2] und [7] ausgeführt.

Die Robustheit dieses Schemas gegenüber Störungen in Form nicht modellierten Systemverhaltens kann mathematisch nachgewiesen werden. Insbesondere ist gesichert, dass das im Schritt 2 gestellte Optimierungsproblem in jedem folgenden Zyklus lösbar bleibt, sofern es im ersten lösbar war. Damit ist die unbeschränkte Ausführbarkeit des Verfahrens gesichert (siehe [5] und [6]).

Zusammenfassung

Die Regelung von physikalischen Systemen erfordert a-priori Wissen, welches durch Systemmodelle
in die Regelungsaufgabe eingeführt wird. Die üblichen Ansätze zur Modellbildung stoßen dabei auf
prinzipielle Grenzen mit wachsender Komplexität des Systems. Sie liefern allerdings während ihrer Erstellung
wesentliche theoretische Einblicke in die Struktur des Systems und benötigen nur wenig experimentelles Vorwissen.

Der vorgestellte datenbasierte Ansatz hingegen generiert eine Systemrepräsentation aus einer einzigen
Beobachtungsreihe, zu deren Gewinnung das System einer spezifischen Anregung ausgesetzt wird.
Die Vollständigkeit der erzeugten Systemrepräsentation kann anhand der bereits gewonnenen Daten
geprüft werden, was eine für ein Lernverfahren bemerkenswerte Eigenschaft darstellt.
Durch dieses Vorgehen unterliegt das Verfahren keinerlei prinzipiellen Einschränkungen hinsichtlich der Systemkomplexität, benötigt stattdessen aber spezielle empirische Daten zur Systembeschreibung.

Obwohl der neue Ansatz kein Modell im eigentlichen Sinne liefert, ist es mit der von ihm erzeugten
Systemrepräsentation möglich, spezifische Vorhersagen zum Systemverhalten zu treffen. Dabei wird nicht nur die Konvergenz gegen einen gewünschten Zielzustand realisiert, sondern werden gleichzeitig eingabe- wie ausgabeseitig technische und physikalische Restriktionen umsetzt. Dies stellt einen signifikanten Vorteil gegenüber anderen Lernverfahren dar und ermöglicht sicherheitskritische Anwendungen im Zusammenspiel mit etablierten Regelungsstrategien wie dem „Model Predictive Control“.

Ausblick

Die Darstellung des neuen datenbasierten Ansatzes hat die Behandlung zweier wesentlicher Probleme ausgespart.

Der erste Aspekt betrifft die Anwendung auf nichtlineare Systeme. Den theoretischen Voraussetzungen nach ist der datenbasierte Ansatz auf lineare zeitinvariante Systeme beschränkt. Einerseits gibt es in jüngster Zeit Versuche wie in [1] oder [4], diese Einschränkung aufzuheben. Andererseits sind die Gründe für die beobachtete erfolgreiche Regelung nichtlinearer Systeme durch das datenbasierte Vorgehen bisher noch nicht verstanden und daher Gegenstand aktueller Forschung, siehe [2].

Der zweite Aspekt bezieht sich auf die Verwendung verrauschter Beobachtungsdaten bei der Rekonstruktion des Systemverhaltens. Auch hier sind bereits wesentliche Fortschritte zur Stabilisierung datenbasierter Ansätze erzielt worden, siehe [2]. Allerdings zeigen sich andere Ansätze zur Systemidentifikation noch als deutlich unempfindlicher gegenüber Rauscheinflüssen.

Insgesamt zeichnet sich das Bild ab, dass aktuelle datenbasierte Verfahren robust gegenüber Bias-Datenfehlern sind, also Daten aus nicht linearen Systemen, und anfälliger hinsichtlich Varianz-Datenfehlern, also Datenrauschen.

Literatur

[1] Ezzat Elokda, Jeremy Coulson, Paul N. Beuchat, John Lygeros, and Florian Dörfler, „Data-enabled predictive control for quadcopters“, International Journal of Robust and Nonlinear Control, 2021

[2] Florian Dörfler, Jeremy Coulson, and Ivan Markovsky, „Bridging direct and indirect data-driven control formulations via regularizations and relaxations“, IEEE Transactions on Automatic Control, 2022

[3] James B. Rawlings, David Q. Mayne, and Moritz M. Diehl, „Model predictive control – theory, computation, and design“, Nob Hill Publishing, 2022

[4] Julian Berberich, Johannes Köhler, Matthias A. Müller, and Frank Allgöwer, „Data-driven model predictive control – closed-loop guarantees and experimental results“, at-Automatisierungstechnik, 2021

[5] Joscha Bongard, Julian Berberich, Johannes Kohler, and Frank Allgower, „Robust stability analysis of a simple data-driven model predictive control approach“, IEEE Transactions on Automatic Control, 2022

[6] Julian Berberich, Johannes Köhler, Matthias A. Müller, and Frank Allgöwer, „Stability in data-driven MPC – an inherent robustness perspective“, IEEE Conference on Decision and Control, 2022

[7] Ivan Markovsky and Florian Dörfler, „Behavioral systems theory in data-driven analysis, signal processing, andcontrol“, Annual Reviews in Control, 2021

Nachdem der erste Artikel der Serie sich mit den allgemeinen Grundbausteinen von Regelungssystemen beschäftigt hat, widmet sich der zweite Artikel der Modellierung des Verhaltens von Systemen. Dabei steht die Differenzierung verschiedener Modellierungsarten im Vordergrund. Den Hauptteil des Artikels bildet die Einführung eines speziellen datengetriebenen Ansatzes, der in jüngster Zeit wachsendes wissenschaftliches Interesse auf sich gezogen hat.

Die Kenntnis des Systemverhaltens, d. h. das Wissen um die quantitative Veränderung der Ausgaben bei Veränderung der Eingaben des Systems, ist eine Grundvoraussetzung für die Systemregelung. Dieses Wissen wird durch Verhaltensmodelle repräsentiert, deren Entwicklung wir in diesem Artikel näher untersuchen wollen.

Ein physikalisches Bespielsystem

Als einfaches physikalisches Beispiel betrachten wir ein sogenanntes ideales ebenes Pendel. Die Pendelmasse wird als punktförmig und an einem masselosen Seil aufgehängt angenommen, alle Reibungskräfte bleiben unberücksichtigt. Die einzige auf die Masse wirkende Kraft ist die Gravitationskraft der Erde (siehe Abbildung 3).

Beispiel – Whitebox Modellierung des Pendelsystems

Ausgangspunkt bilden das zweite Newtonsche Gesetz sowie das Gravitationsgesetz Newtons spezialisiert für Körper nahe der Erdoberfläche .

Für die Bewegung des Pendels ist lediglich die tangential an die Pendelmasse angreifende Kraft zu betrachten, da die radiale Komponente durch das Seil kompensiert wird. Aus dem gleichen Grund ist lediglich die Tangentialbeschleunigung relevant. Unter Verwendung des zeitabhängigen Ablenkungswinkels und der Winkelbeschleunigung (siehe Abbildung 3) sind die Größen und gegeben als

   

mit der Länge des Pendelseils und als der Fallbeschleunigung auf der Erde. Damit ergibt sich aus folgende Differentialgleichung für den Ablenkungswinkel :

Wenn wir zusätzlich den Winkel als klein annehmen, erhalten wir als weitere Vereinfachung

Diese Differentialgleichung kann dazu verwendet werden, das Verhalten des Pendels für jeden Anfangswinkel und jede Anfangsgeschwindigkeit vorherzusagen.

Grey- and Blackbox Modellierung

Dieser Modellierungszugang führt ebenfalls auf Differential- oder Differenzengleichungen, die allerdings lediglich die grundlegende Struktur des Systems vorgeben und daher freie Parameter enthalten. Fließt in das Systemmodell Vorwissen, z. B. in Form von physikalischen Prinzipien ein, so handelt es sich um ein Grey-Box Model, anderenfalls wird von einem Black-Box Model gesprochen.

Die freien Parameter des Modells werden in einem Adaptionsschritt aus Beobachtungsdaten des Systems bestimmt, wobei dieser Schritt der Modellbildung weitgehend automatisiert werden kann. Die Auswahl der Modellstruktur hingegen erweist sich als kritisch für die Qualität des Modells, erfordert aufgrund seiner Komplexität ein hohes Maß an Erfahrung und kann daher nur bedingt automatisiert werden. Darüber hinaus können Grey- und Blackbox Modelling im Gegensatz zum White-Box Ansatz auf beliebig komplexe Systeme angewendet werden.

Daten basierte Modellierung

Dieser neue Ansatz zieht seit einigen Jahren zunehmend Aufmerksamkeit auf sich. Ausgangspunkt ist der Gedanke, ein System ausschließlich mit seinem von außen verifizierbaren Verhalten zu identifizieren. Eine ausführliche Darstellung des systemtheoretischen Hintergrundes für diesen Ansatz findet sich in [1]. Mit der zunehmenden Verfügbarkeit von Prozessdaten technischer Systeme wandelte sich die Sicht auf diese datengetriebene Betrachtungsweise. Es wurde erkannt, dass die Beschreibung des Systemverhaltens rein auf der Basis von Beobachtungen die Tür zu neuen Modellen und Algorithmen öffnete (siehe [2] und [3]). Diese Entwicklung ist vergleichbar mit den Entwicklungen bei der Anwendung von neuronalen Netzen in den vergangenen Jahren.

Da es sich um ein nicht-überwachtes Lernverfahren für nicht-parametrische Modelle handelt, wird im Gegensatz zum White-, Grey- und Black-Box Modelling kein Modell des Systems konstruiert. Damit unterliegt die Anwendbarkeit dieser Herangehensweise weder einer komplexitätsbedingten Einschränkung, noch verhindert die Notwendigkeit einer Strukturentscheidung seine Automatisierung. Allerdings ist es dem Ansatz nach zunächst auf sogenannte lineare und zeitinvariante Systeme beschränkt (siehe „Mathematischer Hintergrund“).

Beispiel – Datenbasierte Modellierung des Pendelsystems

Um eine datenbasierte Repräsentation für das Pendelsystem zu erhalten, benötigen wir lediglich zwei Experimente. Unter Verwendung der Bezeichnung mit dem Ablenkungswinkel und der Winkelgeschwindigkeit können die Anfangsbedingungen für die beiden Experimente angesetzt werden zu

   

Das erste Experiment zeichnet die Bewegung des Pendels zum Startwinkel und verschwindender Startgeschwindigkeit zu diskreten Zeitpunkten auf. Das zweite Experiment verwendet für die Aufzeichung von das dazu inverse Setting.

Aus den Aufzeichnungen der beiden Experimente kann dann jede andere Pendelbewegung zu den Anfangsbedingungen mittels der Beziehung

   

zu den Zeitpunkten berechnet werden, wofür die lineare Unabhängigkeit der Vektoren der beiden Anfangsbedingungen die Grundlage darstellt. In kompakter Form erhalten wir weiter die Darstellung

   

Die Matrix bezeichnen wir als algebraische Repräsentation des Pendelverhaltens.

Die Zielstellung, das vollständige Systemverhalten allein aus Beobachtungsdaten zu rekonstruieren, wirft drei wesentliche Fragen auf:

• Welche Daten eignen sich zur Verhaltensrepräsentation?
• Wie kann diese Eignung überprüft werden?
• Welchen Umfang müssen die gesammelten Daten besitzen?

Die mathematische Theorie gibt hier eindeutige Antworten (siehe „Mathematischer Hintergrund“). Wir wollen uns an dieser Stelle auf die Feststellung beschränken, dass die erhobenen Daten eine mathematisch exakt definierte Unabhängigkeit besitzen müssen (siehe Beispiel – Datenbasierte Modellierung des Pendelsystems). Solche Daten lassen sich nur gewinnen, indem das System in systematischer Art und Weise angeregt wird, da physikalische Systeme natürlicherweise dazu tendieren, ohne solche Störungen nach einiger Zeit in einen Gleichgewichtszustand überzugehen.

Die notwendige Vorgehensweise besteht daher darin, im Beobachtungszeitraum das System mittels zufälliger Eingaben anzuregen und damit ein möglichst breit gefächertes Verhalten in den Ausgaben zu induzieren (siehe Abbildung 4). Dabei ist zu beachten, dass diese Systemanregung unter Einhaltung der technischen Rand- und Grenzbedingungen des Systems erfolgen muss, um eine Destabilisierung mit ggf. schwerwiegenden Konsequenzen zu vermeiden.

In regelmäßigen Abständen wird mittels eines Dimensionskriteriums geprüft, ob die gesammelten Daten die Gesamtheit der möglichen Systemreaktionen bereits erfassen. Diese Prüfung erfordert die Angabe der gewünschten bzw. vermuteten Systemkomplexität (siehe „Mathematischer Hintergrund“), was die Möglichkeit beinhaltet, diese auf ein gewünschtes Maß zu begrenzen. Besitzt die bisher gesammelte Datenmenge noch nicht die geforderte Komplexität, so werden erneut Zufallseingabedaten erzeugt und das Experiment wiederholt.

Im Ergebnis dieses Vorgehens wird aus den gesammelten Beobachtungsdaten eine Systemrepräsentation erzeugt. Neben der dynamischen Anpassbarkeit der Komplexität der Systemrepräsentation ist der entscheidende Vorteil dieses Verfahrens, dass der beschriebene Vorgang vollständig automatisiert und damit bei Bedarf autonom wiederholt werden kann.

Die gewonnene Repräsentation des Systemverhaltens kann nun analog zu dem im Beispiel „Datenbasierte Modellierung des Pendelsystems“ angedeuteten Vorgehen dazu verwendet werden, Vorhersagen zum Systemverhalten zu treffen. Ein Beispiel für die Anwendung des Verfahrens zur Lageregelung von Quadcoptern findet sich in [4].

Mathematischer Hintergrund

Der betrachtete Prozess wird als lineares und zeitinvariantes dynamisches System beschrieben, welches Eingabeparameter, Ausgabegrößen und innere Zustände besitzt und eine Differenzengleichung der Form

   

mit , , and erfüllt.

Das Verhalten des Systems ist definiert als die Menge aller Trajektorien , die zeitbeschränkte Version , bestehend aus Trajektorien der Länge , wird identifiziert mit einem endlich dimensionalen Vektorraum der Dimension

   

Im Rahmen des Identifikationsprozesses wird durch Beobachtung und Anregung des Systems eine Matrix gebildet, deren Spalten Trajektorien der Länge entsprechen. Das Wissen um die Dimension von ermöglicht die Einscheidung zum Stopp der Datenakquise
durch die Überprüfung, ob die bereits gesammelten Spalten von einen hinreichend hochdimensionalen
Unterraum aufspannen.

Die Anzahl der inneren Zustände des Systems gilt als ein Komplexitätsmaß für das zu identifizierende
System und kann dazu verwendet werden, die Komplexiät der empirisch bestimmten Systemrepräsentation
von zu begrenzen, um die Genauigkeit der Approximation den Erfordernissen anzupassen.

Nachdem wir uns mit der Entwicklung von Systemmodellen insbesondere für den rein datengetriebenen Fall vertraut gemacht haben, werden wir uns im folgenden Artikel dem Thema Regelung zuwenden. Dabei wird speziell eine Strategie im Vordergrund stehen, die sich besonders für die Regelung hochkomplexer Systeme eignet, d. h. für Systeme mit einer großen Anzahl an Eingriffs- und Zielgrößen.

Literatur

[1] Jan C. Willems, „Paradigms and puzzles in the theory of dynamical systems“, IEEE Transactions on Automatic Control, 1991

[2] Ivan Markovsky, Linbin Huang, and Florian Dörfler, „Data driven control based on the behavioral approach – from theory to applications in power systems“, IEEE Control Systems, 2022

[3] Ivan Markovsky and Florian Dörfler, „Behavioral systems theory in data-driven analysis, signal processing, and control“, Annual Reviews in Control, 2021

[4] Ezzat Elokda, Jeremy Coulson, Paul N. Beuchat, John Lygeros, and Florian Dörfler, „Data-enabled predictive control for quadcopters“, International Journal of Robust and Nonlinear Control, 2021

Die automatische Regelung von komplexen physikalischen Systemen stellt für Wissenschaftler und Ingenieure eine stetig wachsende theoretische wie technische Herausforderung dar. Dabei ist es zunächst unerheblich, ob diese Systeme biologische oder chemische Reaktoren, Windkraftanlagen, Stromnetze, Flugzeuge oder auch Fertigungssysteme sind. In allen diesen Anwendungsfällen treten ähnliche theoretische wie praktische Fragestellungen auf und wir wollen in diesem Artikel auf einige wesentliche näher eingehen. Bevor wir damit beginnen können, benötigen wir allerdings mehr Vorwissen.

In den nachfolgenden Ausführungen werden wir die relevanten Aspekte zumeist in beschreibender oder grafischer Form diskutieren. In entsprechend abgesetzten Abschnitten erfolgt eine stark gekürzte, skizzenhafte mathematische Beschreibung, die zumindest einen kurzen Einblick in die zugehörigen theoretischen Hintergründe geben soll.

Ein fertigungstechnisches Beispiel

Als Beispiel für ein einfaches zu regelndes System soll eine idealisierte Werkstückbearbeitung auf einer Drehmaschinedienen, wie sie in Abbildung 1 dargestellt ist.

Das zu bearbeitende, rotationssymmetrische Werkstück (1) führt eine Drehbewegung aus, die es ermöglicht, unter Verwendung des Werkzeugs (2) den Durchmesser D des Werkstücks durch Materialabtrag zu verringern. Der Vorschub des Werkzeugs wird gemäß CNC Programm derart gesteuert, dass dieser Abtrag bis zum gewünschten Durchmesser D erfolgt.

Das Werkzeug ist dabei auf einer Aufnahme (3) gelagert, die einen Abstand C vom Rotationszentrum besitzt. Dieser Abstand C kann zur Kompensation der Werkzeugabnutzung angepasst werden.
Wie wir im Folgenden sehen werden, genügt dieses einfache Beispiel, um die wesentlichen Komponenten einer automatischen Regelung im nächsten Abschnitt zu identifizieren.

Grundbausteine von Regelungssystemen

Eine automatische Regelung eines Systems erfordert vier zentrale Komponenten, die zur Lösung dieser Aufgabe zur Verfügung stehen müssen. Die erste Voraussetzung stellt die Definition und automatische Erfassung von Zielgrößen dar, die einer Regelung unterzogen werden sollen. Zum Zweiten muss das System Eingriffsgrößen aufweisen, die es erlauben, diese Zielgrößen zu manipulieren. Drittens ist die Kenntnis des quantitativen Zusammenhanges der Zielgrößen mit den Eingriffsgrößen des Systems erforderlich. Viertens muss eine Strategie zur Anpassung der Eingriffsgrößen vorliegen, welche in der Lage ist, die Zielgrößen in einen a-priori festgelegten Korridor zu steuern und dort zu halten.

Die Abbildung 2 gibt einen Überblick über die für eine automatische Regelung benötigten Grundkomponenten, die wir nachfolgend näher betrachten werden.

• Wahrnehmung

Seit einiger Zeit werden verstärkt Messsysteme direkt in die Fertigungsanlagen und Fertigungsmaschinenintegriert. Auf diese Weise können die im Fertigungsprozess entstehenden Qualitäts- und Prozessdaten in einer Frequenz und Dichte erfasst werden, wie sie für eine effektive Regelung erforderlich ist. Neueste Forschungen versuchen darüber hinaus, diese Messsysteme durch sogenannte virtuelle Messtechnik zu ergänzen bzw. zu ersetzen. Hierbei werden Qualitätsdaten mittels eines digitalen Zwillings des Fertigungsprozesses aus Prozessdaten gewonnen.

In unserem Beispielsystem ist der Durchmesser des Werkstücks nach der Fertigung automatisch, z. B. durcheinen Laserscanner, zu erfassen. In einer komplexeren Ausbaustufe kann eine dreidimensionale Digitalisierung der Werkstückoberfläche erfolgen.

• Regelbarkeit

Die prinzipielle Regel- oder Steuerbarkeit von Fertigungssystemen ist aus praktischen Erwägungen heraus größtenteils gegeben. Es existieren damit für Bediener:innen bereits Eingriffsmöglichkeiten an Fertigungssysteme und -maschinen zur Steuerung qualitätsrelevanter Zielgrößen. Allerdings fehlt es vielfach noch an der Automatisierbarkeit der entsprechenden Eingriffe, da diese oftmals mit sicherheitskritischen Systemen interagieren oder dieser Aspekt schlicht nicht vorgesehen war.

In unserem Beispielsystem ist der Abstand C die notwendige Eingriffsgröße. Durch Änderung von C kann die im CNC Programm hinterlegte Vorschubstrecke an den Werkzeugverschleiß angepasst werden. In der Regel muss diese Änderung aber noch vom Maschinenbediener manuell vorgenommen werden.

• Verhalten

Für die Regelung des Systems ist das Wissen darüber notwendig, wie sich die Zielgrößen des Systems verändern, wenn die Eingriffsgrößen des Systems manipuliert werden. Diese Zusammenhänge werden in Modellen des Systemverhaltens zusammengefasst und können extrem komplex sein, weshalb dieser Aspekt der Regelung eine zentrale Herausforderung darstellt.

In unserem Beispielsystem handelt es sich um den Zusammenhang zwischen dem Abstand C und dem realisierten Durchmesser D. Offenbar ist dieser Zusammenhang linear, da sich das Werkzeug in gleicher Höhe wie die Rotationsachse befindet. Wäre dies nicht der Fall, so würde es sich um einen nichtlinearen Zusammenhang handeln.

• Strategie

Wie aus den obigen Erläuterungen hervorgeht, stellen die Aspekte Verhalten und Strategie eine besondere Herausforderung dar – sowohl in praktischer wie auch in theoretischer Hinsicht. In den beiden folgenden Artikeln werden wir daher diese beiden Themen in den Mittelpunkt stellen. Dabei beschäftigen wir uns im nächsten Artikel unter anderem mit der Möglichkeit einer automatischen Modellierung hochkomplexer technischer Systeme und im letzten Beitrag mit der Entwicklung zugehöriger robuster Regelungsstrategien.