ZEISS Digital Innovation Blog - Datengetriebene Prozessregelung - Teil 2: Modellierung von Systemverhalten

Nachdem der erste Artikel der Serie sich mit den allgemeinen Grundbausteinen von Regelungssystemen beschäftigt hat, widmet sich der zweite Artikel der Modellierung des Verhaltens von Systemen. Dabei steht die Differenzierung verschiedener Modellierungsarten im Vordergrund. Den Hauptteil des Artikels bildet die Einführung eines speziellen datengetriebenen Ansatzes, der in jüngster Zeit wachsendes wissenschaftliches Interesse auf sich gezogen hat.

Die Kenntnis des Systemverhaltens, d. h. das Wissen um die quantitative Veränderung der Ausgaben bei Veränderung der Eingaben des Systems, ist eine Grundvoraussetzung für die Systemregelung. Dieses Wissen wird durch Verhaltensmodelle repräsentiert, deren Entwicklung wir in diesem Artikel näher untersuchen wollen.

Ein physikalisches Bespielsystem

Als einfaches physikalisches Beispiel betrachten wir ein sogenanntes ideales ebenes Pendel. Die Pendelmasse wird als punktförmig und an einem masselosen Seil aufgehängt angenommen, alle Reibungskräfte bleiben unberücksichtigt. Die einzige auf die Masse wirkende Kraft ist die Gravitationskraft der Erde (siehe Abbildung 3).

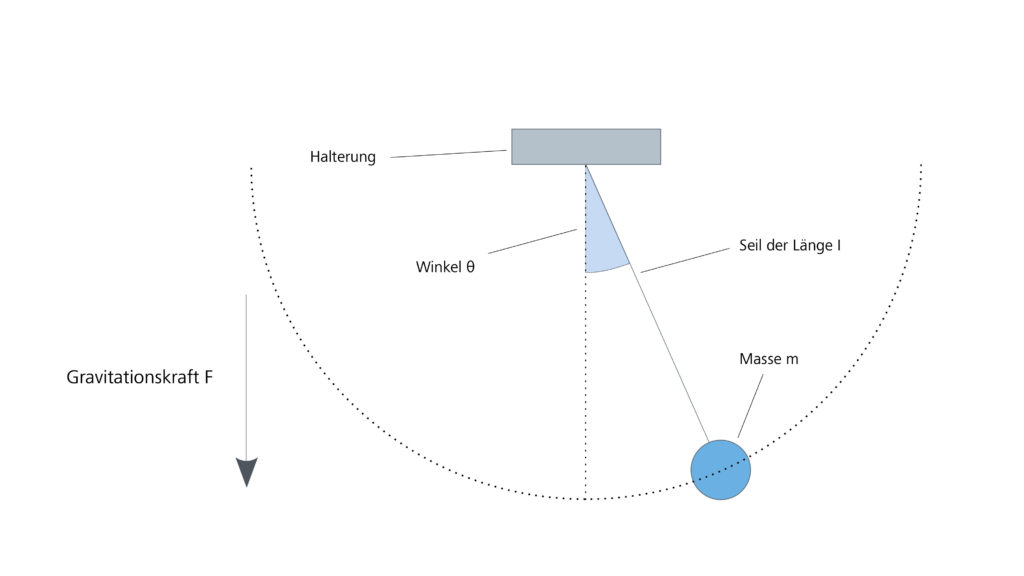
An diesem Beispiel werden wir drei grundlegende Modellierungsarten beschreiben.

Whitebox Modellierung

Bei dieser Art der Modellierung wird das Systemverhalten durch Differentialgleichungen repräsentiert, deren Parameter vollständig bekannt sind. Der Ansatz ist hochgradig anwendungsfallspezifisch und erfordert ein hohes Maß an Detailwissen zum betrachteten System. Die Komplexität realer Systeme setzt der Anwendung dieses Ansatzes natürlicherweise Grenzen. Zusätzlich ist die Herangehensweise schwer automatisierbar und die erhaltenen Modelle sind nur mit großem Aufwand an veränderte Anforderungen anpassbar.

Beispiel – Whitebox Modellierung des Pendelsystems

Ausgangspunkt bilden das zweite Newtonsche Gesetz $F = m \, a$ sowie das Gravitationsgesetz Newtons spezialisiert für Körper nahe der Erdoberfläche $F = m \, g \, [\, 0, -1 \,]^T$ .

Für die Bewegung des Pendels ist lediglich die tangential an die Pendelmasse angreifende Kraft $F_T$ zu betrachten, da die radiale Komponente durch das Seil kompensiert wird. Aus dem gleichen Grund ist lediglich die Tangentialbeschleunigung $a_T$ relevant. Unter Verwendung des zeitabhängigen Ablenkungswinkels $\theta(t)$ und der Winkelbeschleunigung $\ddot{\theta}(t)$ (siehe Abbildung 3) sind die Größen $F_T$ und $a_T$ gegeben als

$F_T = -m \ g \sin \theta(t) \quad \text{und} \quad a_T(t) = l \, \ddot{\theta}(t)$

mit der Länge $l$ des Pendelseils und $g \approx 9.81 \frac{m}{s^2}$ als der Fallbeschleunigung auf der Erde. Damit ergibt sich aus $m \ a_T = F_T$ folgende Differentialgleichung für den Ablenkungswinkel $\theta$ :

$\ddot{\theta} (t) = - \frac{g}{l} \ \sin \theta(t)$

Wenn wir zusätzlich den Winkel $\theta$ als klein annehmen, erhalten wir als weitere Vereinfachung

$\ddot{\theta} (t) = - \frac{g}{l} \ \theta(t)$

Diese Differentialgleichung kann dazu verwendet werden, das Verhalten des Pendels für jeden Anfangswinkel $\theta_0 \ll 1$ und jede Anfangsgeschwindigkeit $\dot{\theta}_0$ vorherzusagen.

Grey- and Blackbox Modellierung

Dieser Modellierungszugang führt ebenfalls auf Differential- oder Differenzengleichungen, die allerdings lediglich die grundlegende Struktur des Systems vorgeben und daher freie Parameter enthalten. Fließt in das Systemmodell Vorwissen, z. B. in Form von physikalischen Prinzipien ein, so handelt es sich um ein Grey-Box Model, anderenfalls wird von einem Black-Box Model gesprochen.

Die freien Parameter des Modells werden in einem Adaptionsschritt aus Beobachtungsdaten des Systems bestimmt, wobei dieser Schritt der Modellbildung weitgehend automatisiert werden kann. Die Auswahl der Modellstruktur hingegen erweist sich als kritisch für die Qualität des Modells, erfordert aufgrund seiner Komplexität ein hohes Maß an Erfahrung und kann daher nur bedingt automatisiert werden. Darüber hinaus können Grey- und Blackbox Modelling im Gegensatz zum White-Box Ansatz auf beliebig komplexe Systeme angewendet werden.

Daten basierte Modellierung

Dieser neue Ansatz zieht seit einigen Jahren zunehmend Aufmerksamkeit auf sich. Ausgangspunkt ist der Gedanke, ein System ausschließlich mit seinem von außen verifizierbaren Verhalten zu identifizieren. Eine ausführliche Darstellung des systemtheoretischen Hintergrundes für diesen Ansatz findet sich in [1]. Mit der zunehmenden Verfügbarkeit von Prozessdaten technischer Systeme wandelte sich die Sicht auf diese datengetriebene Betrachtungsweise. Es wurde erkannt, dass die Beschreibung des Systemverhaltens rein auf der Basis von Beobachtungen die Tür zu neuen Modellen und Algorithmen öffnete (siehe [2] und [3]). Diese Entwicklung ist vergleichbar mit den Entwicklungen bei der Anwendung von neuronalen Netzen in den vergangenen Jahren.

Da es sich um ein nicht-überwachtes Lernverfahren für nicht-parametrische Modelle handelt, wird im Gegensatz zum White-, Grey- und Black-Box Modelling kein Modell des Systems konstruiert. Damit unterliegt die Anwendbarkeit dieser Herangehensweise weder einer komplexitätsbedingten Einschränkung, noch verhindert die Notwendigkeit einer Strukturentscheidung seine Automatisierung. Allerdings ist es dem Ansatz nach zunächst auf sogenannte lineare und zeitinvariante Systeme beschränkt (siehe „Mathematischer Hintergrund“).

Beispiel – Datenbasierte Modellierung des Pendelsystems

Um eine datenbasierte Repräsentation für das Pendelsystem zu erhalten, benötigen wir lediglich zwei Experimente. Unter Verwendung der Bezeichnung $x(t) = [\, \theta(t), \dot{\theta}(t) \, ]^T$ mit dem Ablenkungswinkel $\theta(t)$ und der Winkelgeschwindigkeit $\dot{\theta}(t)$ können die Anfangsbedingungen für die beiden Experimente angesetzt werden zu

$x_1(0) = \left[ \begin{array}{c} 1 \\ 0 \end{array} \right] \quad \text{und} \quad x_2(0) = \left[ \begin{array}{c} 0 \\ 1 \end{array} \right]$

Das erste Experiment zeichnet die Bewegung $x_1(t)$ des Pendels zum Startwinkel $1^{\circ}$ und verschwindender Startgeschwindigkeit zu diskreten Zeitpunkten $\{ t_i \}_{i=1}^n$ auf. Das zweite Experiment verwendet für die Aufzeichung von $x_2(t)$ das dazu inverse Setting.

Aus den Aufzeichnungen der beiden Experimente kann dann jede andere Pendelbewegung $x(t)$ zu den Anfangsbedingungen $x(0) = [\, \theta_0, \dot{\theta}_0 \,]^T$ mittels der Beziehung

$x(t) = \theta_0 \ x_1(t) + \dot{\theta}_0 \ x_2(t)$

zu den Zeitpunkten $\{ t_i \}_{i=1}^n$ berechnet werden, wofür die lineare Unabhängigkeit der Vektoren der beiden Anfangsbedingungen die Grundlage darstellt. In kompakter Form erhalten wir weiter die Darstellung

$B \, x(0) = x \quad \text{mit} \quad B = \begin{bmatrix} x_1(t_1) & x_2(t_1) \\ \vdots & \vdots \\ x_1(t_n) & x_2(t_n) \end{bmatrix} \quad \text{und} \quad x = \begin{bmatrix} x(t_1) \\ \vdots \\ x(t_n) \end{bmatrix}$

Die Matrix $B$ bezeichnen wir als algebraische Repräsentation des Pendelverhaltens.

Die Zielstellung, das vollständige Systemverhalten allein aus Beobachtungsdaten zu rekonstruieren, wirft drei wesentliche Fragen auf:

Welche Daten eignen sich zur Verhaltensrepräsentation?
Wie kann diese Eignung überprüft werden?
Welchen Umfang müssen die gesammelten Daten besitzen?

Die mathematische Theorie gibt hier eindeutige Antworten (siehe „Mathematischer Hintergrund“). Wir wollen uns an dieser Stelle auf die Feststellung beschränken, dass die erhobenen Daten eine mathematisch exakt definierte Unabhängigkeit besitzen müssen (siehe Beispiel – Datenbasierte Modellierung des Pendelsystems). Solche Daten lassen sich nur gewinnen, indem das System in systematischer Art und Weise angeregt wird, da physikalische Systeme natürlicherweise dazu tendieren, ohne solche Störungen nach einiger Zeit in einen Gleichgewichtszustand überzugehen.

Die notwendige Vorgehensweise besteht daher darin, im Beobachtungszeitraum das System mittels zufälliger Eingaben anzuregen und damit ein möglichst breit gefächertes Verhalten in den Ausgaben zu induzieren (siehe Abbildung 4). Dabei ist zu beachten, dass diese Systemanregung unter Einhaltung der technischen Rand- und Grenzbedingungen des Systems erfolgen muss, um eine Destabilisierung mit ggf. schwerwiegenden Konsequenzen zu vermeiden.

Abbildung 4: Zufällige Eingaben zur Exploration des Systemverhaltens

In regelmäßigen Abständen wird mittels eines Dimensionskriteriums geprüft, ob die gesammelten Daten die Gesamtheit der möglichen Systemreaktionen bereits erfassen. Diese Prüfung erfordert die Angabe der gewünschten bzw. vermuteten Systemkomplexität (siehe „Mathematischer Hintergrund“), was die Möglichkeit beinhaltet, diese auf ein gewünschtes Maß zu begrenzen. Besitzt die bisher gesammelte Datenmenge noch nicht die geforderte Komplexität, so werden erneut Zufallseingabedaten erzeugt und das Experiment wiederholt.

Im Ergebnis dieses Vorgehens wird aus den gesammelten Beobachtungsdaten eine Systemrepräsentation erzeugt. Neben der dynamischen Anpassbarkeit der Komplexität der Systemrepräsentation ist der entscheidende Vorteil dieses Verfahrens, dass der beschriebene Vorgang vollständig automatisiert und damit bei Bedarf autonom wiederholt werden kann.

Die gewonnene Repräsentation des Systemverhaltens kann nun analog zu dem im Beispiel „Datenbasierte Modellierung des Pendelsystems“ angedeuteten Vorgehen dazu verwendet werden, Vorhersagen zum Systemverhalten zu treffen. Ein Beispiel für die Anwendung des Verfahrens zur Lageregelung von Quadcoptern findet sich in [4].

Mathematischer Hintergrund

Der betrachtete Prozess wird als lineares und zeitinvariantes dynamisches System $S$ beschrieben, welches $m$ Eingabeparameter, $p$ Ausgabegrößen und $n$ innere Zustände besitzt und eine Differenzengleichung der Form

$\begin{aligned} x(k+1) &= A \, x(k) + B \, u(k) \\[0.5em] y(k) &= C \, x(k) + D \, u(k) \end{aligned}$

mit $x(k) \in \mathbb{R}^n$ , $u(k) \in \mathbb{R}^m$ , and $y(k) \in \mathbb{R}^p$ erfüllt.

Das Verhalten $B$ des Systems ist definiert als die Menge aller Trajektorien $w = (u, y)$ , die zeitbeschränkte Version $B_L$ , bestehend aus Trajektorien der Länge $L$ , wird identifiziert mit einem endlich dimensionalen Vektorraum der Dimension

$\dim B_L = m L + n.$

Im Rahmen des Identifikationsprozesses wird durch Beobachtung und Anregung des Systems $S$ eine Matrix $H_L$ gebildet, deren Spalten Trajektorien der Länge $L$ entsprechen. Das Wissen um die Dimension von $B_L$ ermöglicht die Einscheidung zum Stopp der Datenakquise
durch die Überprüfung, ob die bereits gesammelten Spalten von $H_L$ einen hinreichend hochdimensionalen
Unterraum aufspannen.

Die Anzahl $n$ der inneren Zustände des Systems $S$ gilt als ein Komplexitätsmaß für das zu identifizierende
System und kann dazu verwendet werden, die Komplexiät der empirisch bestimmten Systemrepräsentation
$H_L$ von $B_L$ zu begrenzen, um die Genauigkeit der Approximation den Erfordernissen anzupassen.

Nachdem wir uns mit der Entwicklung von Systemmodellen insbesondere für den rein datengetriebenen Fall vertraut gemacht haben, werden wir uns im folgenden Artikel dem Thema Regelung zuwenden. Dabei wird speziell eine Strategie im Vordergrund stehen, die sich besonders für die Regelung hochkomplexer Systeme eignet, d. h. für Systeme mit einer großen Anzahl an Eingriffs- und Zielgrößen.

Literatur

[1] Jan C. Willems, „Paradigms and puzzles in the theory of dynamical systems“, IEEE Transactions on Automatic Control, 1991

[2] Ivan Markovsky, Linbin Huang, and Florian Dörfler, „Data driven control based on the behavioral approach – from theory to applications in power systems“, IEEE Control Systems, 2022

[3] Ivan Markovsky and Florian Dörfler, „Behavioral systems theory in data-driven analysis, signal processing, and control“, Annual Reviews in Control, 2021

[4] Ezzat Elokda, Jeremy Coulson, Paul N. Beuchat, John Lygeros, and Florian Dörfler, „Data-enabled predictive control for quadcopters“, International Journal of Robust and Nonlinear Control, 2021

Dieser Beitrag wurde verfasst von:

Dr. Daniel Görsch

Dr. Daniel Görsch arbeitet seit April 2022 als Senior-Software Developer bei der ZEISS Digital Innovation. Für die Realisierung von Advanced Manufacturing Lösungen greift er auf mehr als 20 Jahre Erfahrung in Forschung und Softwareentwicklung mit den Schwerpunkten nichtlineare Optimierung, statistische Prozessanalyse und dimensionelle Messtechnik zurück. Aktuell gilt sein Interesse datengetriebenen Methoden zur Repräsentation und Regelung dynamischer Systeme und deren Anwendung auf Fertigungsprozesse.

Alle Beiträge des Autors anzeigen