A not inconsiderable part of the work of a software architect consists of comparing different solution alternatives with each other. Decision tables or evaluation matrices are often used for this purpose, whereby both terms are usually used synonymously. This article aims to provide an insight into two basic approaches and to evaluate them according to their suitability.

Types of evaluation matrices
Evaluation methods for comparing several options range from simple rankings based on voting to complicated evaluation methods based on matrices calculations. The challenge is to find the most appropriate methodology for an objectified evaluation of the comparison of two options available. Criteria for this are:
- Fast comparison
- Simple, uncomplicated procedure
- Little to no training time
- Any number of people
After a brief comparison of the evaluation methods based on the criteria mentioned, the very widespread and well-known utility value analysis turns out to be the method of choice here. Why? Because it is an uncomplicated and simple way of comparing options on the basis of various criteria without the need for a great deal of mathematical effort. In the utility value analysis, the variants are evaluated with a score using weighted criteria, the weighting and score are multiplied together and all the evaluations for an option are added up (see example).
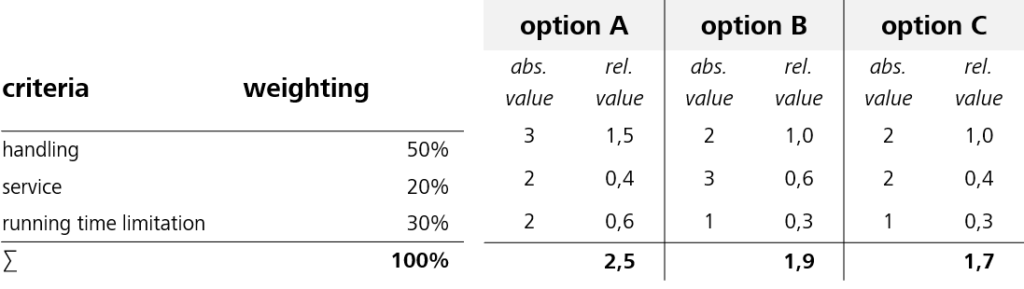
This procedure should be familiar to almost everyone and is also used in practice in many areas. In addition to the evaluation by the person giving the score, there is a potential source of subjective error: the weighting of the criteria. Since score allocation cannot be made more objective, a way of calculating the weighting objectively must be found. This is absolutely essential if a meaningful utility value analysis is required. Objective weighting ensures that no “mindless” decisions are made, e.g. due to time pressure, and that the weighting is as independent of the observer as possible.
Procedure for calculating weighting
As with the utility value analysis, the procedure should be uncomplicated, quick and require no training. Under these premises, two procedures in particular emerge, which are briefly explained in the following below.
Graduated weighting
In the graduated weighting calculation, all criteria are compared with each other in terms of their importance. Thereby, the scale comprises five gradations from -2: “significantly lower importance” to 2: “significantly higher importance”. This granular assessment must therefore be made for each pairing of criteria. The weighting is then calculated using a method similar to matrices calculation.

Priority weighting
Here, the granular evaluation is dispensed with and a distinction is only made between “more important” and “less important”. Thus, each criterion is compared with each other and the more important one is noted in the table. The relative proportion of the number of a criterion is then used to determine the weighting. This procedure can be integrated well in a team, because after the ranking by the individuals, all results can be combined and thus a representative weighting is obtained.

When is which procedure suitable?
In principle, any weighting procedure can be used in any situation. However, the following table gives indications for which calculation method can be advantageous in which circumstances.
| Graduated weighting | Priority weighting |
| Low number of criteria | High number of criteria |
| Low number of evaluating persons | High number of evaluating persons |
| Sufficient time available | Little time available |
| Especially important decision |
In summary, it can be said that the procedure of graduated weighting is often too labour-intensive if one assumes in practice that decisions are sometimes not even accompanied by a representative evaluation procedure. Priority weighting, on the other hand, is an uncomplicated option that can be quickly understood and also implemented in a team and is therefore particularly recommended.
In addition to the utility value analysis, other methods and indicators can be used to compare variants, such as standard deviation, number of gains/losses, etc., which should make the final decision easier, but which are not part of this article.