In his research, Daniel Kahnemann, Nobel Prize laureate for economics in 2002, documented systematic errors in human thought and attributed them not to distortion by emotions, but to the construction of our cognition. In this context, the question of how AI-based systems can compensate for the deficiencies of human reasoning when dealing with statistical or incomplete data is of interest. This is particularly true in areas where wrong decisions have far-reaching consequences, such as medicine.
Modelling application examples
As part of my thesis in computer science, we modelled application examples for the processing of uncertain knowledge from the biomedical field using qualitativeconditionals. With the help of qualitative conditionals, rules of the form “If A, then mostly B” can be encoded as (B|A). Such rules express a plausible, but not necessarily certain, relationship between A and B.
The knowledge we use to draw conclusions is represented by a knowledge base. This consists of conditionals. For example, the knowledge base of Rbirds = { (f|b), (b|p) , (¬f|p) , (w|b) } should represent our knowledge of penguins (p), birds (b), the property of having wings (w) and the ability to fly (f). We know that: (f|b) – birds fly, (b|p) – penguins are birds, (¬f|p) – penguins do not fly and (w|b) – birds have wings. The problem with this knowledge base from the point of view of a classical logic is, that it allows to draw contradictory conclusions: On the one hand, penguins being birds can fly, at the same time, they can’t.
The ranking functions provide a remedy here. They make it possible to assess different scenarios on the basis of available knowledge according to their plausibility. In addition, it is possible – contrary to classical logic – to revise conclusions already drawn. Either because there are certain exceptions to the rules, or because the knowledge changes. Penalty points are assigned to each of the conditionals, which express how much it costs if a scenario violates the conditional. For our knowledge base Rbirds , for example, the scenario pbfw (A world in which penguins are birds, have wings and fly) violates the second rule (¬f|p) and is therefore less plausible than the scenario pb¬fw (A world where penguins are birds, have wings and do not fly).

Conclusion of the intelligent agent
Our intelligent agent was able to follow three strategies in drawing conclusions based on different mathematical systems whose labels have evolved historically:
- In the case of System P, conclusions are drawn over all the rankings allowed for the knowledge base R. It therefore draws its conclusions very cautiously.
- In System Z, the ranking of a scenario is only affected by the value of the highest exceptional rule violated by that scenario. It does not allow the inheritance of the properties of a superior class in subclasses that have exceptional properties.
- In general C-Representations, the rank of a scenario is influenced by all the rules that are violated. The minimum C-representations, on the other hand, provide the minimum implausibility levels of the scenarios, whereby three different minimality measures (cw, sum, ind) exist. Furthermore, one can draw conclusions using either skeptical, weakly–skeptical or credulous type of reasoning.
Here is an application example: Malaria tropica is a widespread and life-threatening disease in sub-Saharan Africa. It is caused by an infection with a single-celled parasite, Plasmodiumfalciparum. The malaria pathogen is transmitted by Anopheles mosquitoes. But not everyone infected with P. falciparum gets malaria: Some humans carry a hereditary form of the haemoglobin gene called sickle cell allele. Two copies of this defect gene cause a malformation of the red blood cells and sickle cell anaemia in humans, whereas one copy does not affect the function of red blood cells. However, humans carrying one copy of the sickle cell gene usually do not get seriously sick with malaria despite being infected with the malaria pathogen, thus having a survival advantage against malaria fatality over humans with normal haemoglobin. Strikingly, the sickle cell gene is relatively common in malaria regions: In Africa, for example, there are areas where almost one third of the population carries the mutated haemoglobin gene. The two most important strategies to prevent malaria are the avoidance of mosquito bites and therefore infections (exposure prophylaxis) and the use of medication to control the spread of the malaria pathogen inside the body after an infection (chemoprophylaxis). Since the malaria pathogen is constantly changing genetically, it is always to be expected that it develops resistance to common drugs.
To model the outcome of a malaria disease in an infected patient h, we used the signature Σ = {h, m, s, p, r} with the following semantics. The variable h represents the patients infected with the malaria pathogen. The variable m is true if the infected patient gets sick with malaria. The variable s expresses that the patient carries a copy of the sickle cell gene. An applied chemoprophylaxis is modelled by p and an infection with a resistant pathogen is modelled by r. The KBmalaria knowledge base contained:
- (¬s| h) Infected patients usually do not have a sickle cell gene.
- (m|¬s) A lack of sickle cell gene usually allows to become seriously sick with malaria.
- (¬m|s) A sickle cell gene usually does not allow to become seriously sick with malaria.
- (¬m|p) Applying chemoprophylaxis usually does not allow to develop severe malaria.
- (m|pr) Applying chemoprophylaxis and the pathogen resistance to it usually allows to develop severe malaria.
We have confronted the knowledge base of our agent with i. a. the following questions:
- (m|h) Do patients, infected with the malaria pathogen, usually get seriously sick with malaria?
- (m|hpr) Does a patient who got a malaria prophylaxis and is infected with a resistant malaria pathogen usually get seriously sick with malaria?
- (m|hprs) Does a patient who got a malaria prophylaxis, is infected with a resistant malaria pathogen and has a sickle cell gene usually get seriously sick with malaria?
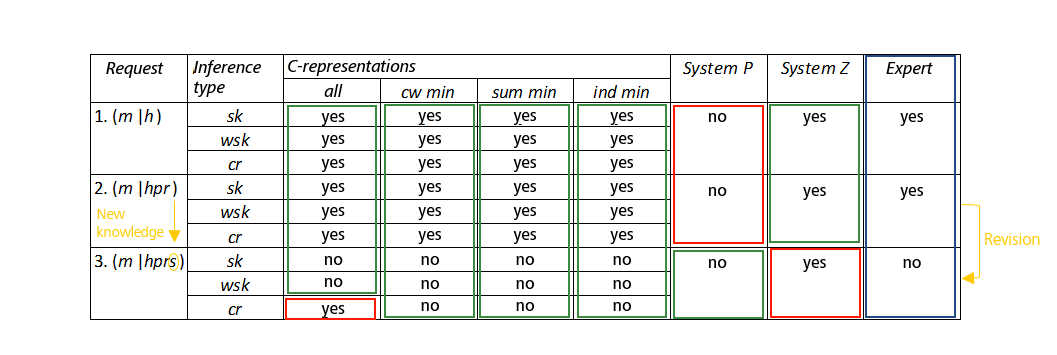
The first question is to be answered by the AI agent with a “yes”, since infected people usually do not have a sickle cell gene, and therefore become seriously sick with malaria. The second question should also be answered with a “yes”. The last question is the most interesting one, since it involves balancing two contradictory arguments of the knowledge base: On the one hand, infected people become seriously sick with malaria when they use chemoprophylaxis, and the malaria pathogen is resistant to it. On the other hand, a sickle cell gene protects against a severe course of the disease. Empirically, the second argument weighs more heavily since a sickle cell gene also protects against prophylaxis-resistant malaria pathogens. The comparison between the second and the third question shows that individual systems of the agent allow for revisable reasoning: If we add s to our request, we can no longer reason m.
Conclusion
We were able to show how biomedical knowledge can be expressed using qualitative conditional logic. Here we found that, especially in the case of skeptical and weakly-skeptical reasoning using C-representations, the answers of the intelligent agent matched the answers of a human expert, demonstrating that revisable reasoning is possible for machines. Since the underlying algorithms have to be optimized, the potential of this AI approach will only become apparent in the future. If sufficient large knowledge bases can be processed algorithmically, it is to be assumed that such an AI agent can also provide useful support to human experts.
Systems based on qualitative conditionals permit the revision of conclusions in the case of changing state of knowledge, which is particularly important in the medical field. In contrast to the probability-based results of quantitative modelling, the user receives a clear yes- or no-answer to their question. In comparison to neural networks, the conclusion of such a system can be made more transparent, since rule-based modelling makes it easy to understand how it works.
Literature
1) J. Haldimann, A. Osiak, C. Beierle. Modelling and Reasoning in Biomedical Applications with Qualitative Conditional Logic. 10.1007/978-3-030-58285-2_24. (2020)
2) D. Kahneman. Thinking, fast and slow. New York: Farrar, Straus and Giroux. (2011) 3) J. Pearl, D. Mackenzie. The Book of Why: The New Science of Cause. Basic Books (2018)
3) J. Pearl, D. Mackenzie. The Book of Why: The New Science of Cause. Basic Books (2018)