Data-driven Process Control – Part 3: Controlling System Behaviour

This third and last part of the article series on data-driven process control provides an introduction to approaches for controlling systems. The focus is on the classic “model-predictive-control” scheme, which is combined with the results for system modeling from the second article to form a purely data-driven control strategy.

There are numerous theoretical and practical approaches to controlling systems. One of the simplest is the PID controller, which is used in applications such as motor and temperature control, charge control for solar systems or control units for power electronics.

However, we want to look at a more advanced control strategy for a wider range of applications, namely “Model Predictive Control (MPC)” (see [3] and [4]). As is evident from the name, this strategy presupposes the ability to predict the behaviour of the system. A requirement that can be fulfilled by modelling as described in the previous section, but also by the data-based approach presented.

The purpose of the control strategy is to control the output target variables by modifying the intervention variables so that the former remain in a range determined by reference data.

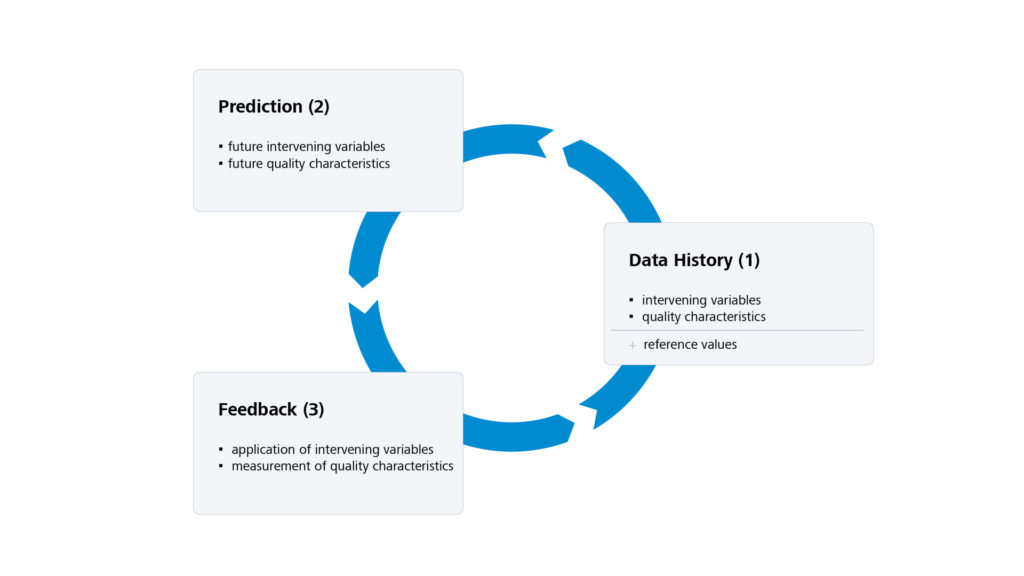
Figure 1: The Model Predictive Control (MPC) Scheme

The MPC strategy is an iterative process consisting of the following three phases (see also Figure 1).

  1. The starting point is the historical data of the system to be controlled. This consists, firstly, of the values of the intervention parameters in previous control steps and, secondly, of the associated output data provided by the system. Since the reference data can also change over time, this makes up part of the historical data as well. This data base represents the status quo of the system under consideration. Any prediction of system behaviour must fit seamlessly into this history.
  2. Starting with the existing system state, the model of the system is used to calculate an optimal prediction of future intervention variables and associated outputs. In this context, the decisive optimisation criterion is the requirement that the output of the system approximates the desired reference values as closely as possible in the prediction period under consideration (see “Mathematical background”). In addition, the technical boundary and limit conditions of the intervention parameters must be taken into account.
  3. The third and final step is to apply the calculated intervention variables in the system itself. This takes the form of a practical test of the model used for prediction. Furthermore, the predicted intervention variables are not applied over the entire prediction horizon, but only for a few steps. This is done in the knowledge that any influences not taken into account by the model will falsify the feedback and thus limit the accuracy of the predictions. At the same time, the feedback ensures the robustness of the strategy, as the newly acquired data is incorporated into the data history and thus forms the updated basis for the next prediction.

The three phases described are run through cyclically. The frequency of this process is directly dependent on the requirements of the particular application. Especially in the case of controlling real-time systems such as vehicles and aircraft, frequencies in the 10 Hz range or beyond are necessary.

Mathematical background

The central element of the “Model Predictive Control” scheme is the prediction of future input parameters u_f and output variables y_f, which minimise the distance to a reference trajectory w_r = (u_r, y_r) in the prediction time horizon T_f. In addition, historical data is given in the form of an initial trajectory w_\text{ini} = (u_\text{ini}, y_\text{ini}) of length T_\text{ini}, which is to be extended by the sought trajectory w_f = (u_f, y_f).

Figure 2: Prediction in the Model Predictive Control scheme

Since the algebraic representation H_L of the time-restricted behaviour B_L allows to determine a vector g for each w \in B_L, to which H_L \, g = w applies, we can formulate the following constrained optimisation problem for w_f

    \[\begin{aligned} &\underset{g}{\text{minimize}} \quad \| H_{T_f} \ g - w_r \|^2_2 & \\[1.0em] &\text{subject to} \quad H_{T_\text{ini}} \ g = w_\text{ini}, & \end{aligned}\]

using the decomposition

    \[H_L \, g = w \quad \Longleftrightarrow \quad \begin{bmatrix} H_{T_\text{ini}} \\[0.5em] H_{T_f} \end{bmatrix} \, g= \begin{bmatrix} w_\text{ini} \\[0.5em] w_f \end{bmatrix}\]

The constraint ensures compliance with the initial condition and the use of H_{T_f} \ g in the minimisation functional ensures that the determined future trajectory w_f = H_{T_f} \ g is permissible for the system S. In addition, constraints on w_f can be formulated, which was not done in this case for reasons of clarity. Further details are provided in [2] and [7].

The robustness of this scheme to disturbances in the form of non-modelled system behaviour can be proven mathematically. In particular, it is ensured that the optimisation problem posed in step 2 remains solvable in each subsequent cycle, provided it was solvable in the first cycle. This guarantees that the procedure can be carried out without any restrictions (see [5] and [6]).

Summary

Control of physical systems requires a priori knowledge, which is introduced into the control task by system models. Conventional approaches to modelling encounter fundamental limits as the complexity of the system increases. However, they provide essential theoretical insights into the structure of the system during their creation and require only little prior experimental knowledge.

The data-based approach presented here, on the other hand, generates a system representation from a single series of observations obtained by subjecting the system to a specific type of stimulation. The completeness of the system representation generated can be checked against the data already obtained, which is a remarkable feature for a learning procedure. This approach means that the method is not subject to any fundamental restrictions with regard to system complexity, but instead requires special empirical data for system description purposes.

Although the new approach does not deliver a model in the true sense, the system representation it generates allows specific predictions to be made about the system’s behaviour. Not only is convergence towards a desired target state achieved, but technical and physical restrictions are also implemented on the input and output sides. This represents a significant advantage over other learning methods and facilitates safety-critical applications in conjunction with established control strategies such as “Model Predictive Control”.

Outlook

The presentation of the new data-based approach has left out the treatment of two major problems.

The first aspect concerns the application to non-linear systems. According to theoretical requirements, the data-based approach is limited to linear time-invariant systems. On the one hand, there have been recent attempts, as in [1] or [4], to overcome this limitation. On the other hand, the reasons why the data-based approach has proven successful in controlling non-linear systems are not yet understood and are therefore the subject of current research, see [2].

The second aspect relates to the use of noisy observation data in the reconstruction of system behaviour. Here, too, significant progress has already been made towards stabilising data-based approaches, see [2]. Nevertheless, other approaches to system identification are still proving to be far less sensitive to noise influences.

Overall, the picture emerges that current data-based methods are robust against bias data errors, i.e. data from non-linear systems, and more vulnerable to variance data errors, i.e. data noise.

Literature

[1] Ezzat Elokda, Jeremy Coulson, Paul N. Beuchat, John Lygeros, and Florian Dörfler, “Data-enabled predictive control for quadcopters”, International Journal of Robust and Nonlinear Control, 2021

[2] Florian Dörfler, Jeremy Coulson, and Ivan Markovsky, “Bridging direct and indirect data-driven control formulations via regularizations and relaxations”, IEEE Transactions on Automatic Control, 2022

[3] James B. Rawlings, David Q. Mayne, and Moritz M. Diehl, “Model predictive control – theory, computation, and design”, Nob Hill Publishing, 2022

[4] Julian Berberich, Johannes Köhler, Matthias A. Müller, and Frank Allgöwer, “Data-driven model predictive control – closed-loop guarantees and experimental results”, at-Automatisierungstechnik, 2021

[5] Joscha Bongard, Julian Berberich, Johannes Kohler, and Frank Allgower, “Robust stability analysis of a simple data-driven model predictive control approach”, IEEE Transactions on Automatic Control, 2022

[6] Julian Berberich, Johannes Köhler, Matthias A. Müller, and Frank Allgöwer, “Stability in data-driven MPC – an inherent robustness perspective”, IEEE Conference on Decision and Control, 2022

[7] Ivan Markovsky and Florian Dörfler, “Behavioral systems theory in data-driven analysis, signal processing, andcontrol”, Annual Reviews in Control, 2021

This post was written by:

Dr. Daniel Görsch

Dr. Daniel Görsch joined ZEISS Digital Innovation in April 2022 as a Senior Software Developer. For the realization of advanced manufacturing solutions, he draws on more than 20 years of experience in research and software development with a focus on non-linear optimization, statistical process analysis and dimensional metrology. His current interest is data-driven methods for representing and controlling dynamic systems and their application to manufacturing processes.

See author's posts