Ein neuer KI-Ansatz zur Modellierung unsicheren Wissens in der Medizin

Daniel Kahnemann, Nobelpreisträger 2002 für Wirtschaftswissenschaften, dokumentierte in seiner Forschungsarbeit systematische Fehler im menschlichen Denken und führte diese nicht auf eine Verfälschung durch Emotionen, sondern auf die Konstruktion unserer Kognition zurück. Interessant ist in diesem Zusammenhang die Frage, wie KI-basierte Systeme die Defizite des menschlichen Schlussfolgerns im Umgang mit statistischen oder unvollständigen Daten ausgleichen können. Dies gilt insbesondere in Bereichen, in denen falsche Entscheidungen weitreichende Folgen haben – wie beispielsweise in der Medizin.

Modellierung der Anwendungsbeispiele

Im Rahmen meiner Abschlussarbeit in Informatik haben wir Anwendungsbeispiele für die Verarbeitung unsicheren Wissens aus dem biomedizinischen Bereich mit qualitativen Konditionalen modelliert. Mithilfe qualitativer Konditionale lassen sich Regeln der Form „Wenn A, dann meistens B“ als (B|A) kodieren. Solche Regeln drücken einen plausiblen, aber nicht zwingend sicheren Zusammenhang zwischen A und B aus.

Das Wissen, das wir zum Schlussfolgern verwenden, wird durch eine Wissensbasis repräsentiert. Diese besteht aus Konditionalen. Beispielsweise soll die Wissensbasis R_birds = { (f|b), (b|p), (¬f|p), (w|b) } unser Wissen über Pinguine (p), Vögel (b), die Eigenschaft Flügel zu besitzen (w) sowie die Fähigkeit zum Fliegen (f) verdeutlichen. Wir wissen, dass: (f|b) – Vögel fliegen, (b|p) – Pinguine Vögel sind, (¬f|p) – Pinguine nicht fliegen und (w|b) – Vögel Flügel haben. Diese Wissensbasis lässt allerdings aus Sicht der klassischen Logik widersprüchliche Schlüsse zu: Zum einen, dass Pinguine als Vögel fliegen können und gleichzeitig, dass sie nicht fliegen können.

Abhilfe schaffen hier die Rangfunktionen.Sie ermöglichen es, verschiedene Szenarien auf Basis vorliegenden Wissens nach ihrer Plausibilität zu beurteilen. Zudem ist es – anders als in der klassischen Logik – möglich, bereits gezogene Schlüsse zu revidieren. Sei es, weil gewisse Ausnahmen von den Regeln existieren, oder sich das Wissen ändert. Jedem der Konditionale werden Strafpunkte zugewiesen, die ausdrücken, wieviel es kostet, wenn ein Szenario das Konditional verletzt. Für unsere Wissensbasis R_birds verletzt z. B. das Szenario pbfw (Eine Welt, in der Pinguine Vögel sind, Flügel haben und fliegen) die zweite Regel (¬f|p) und ist daher unplausibler als das Szenario pb¬fw (Eine Welt, in der Pinguine Vögel sind, Flügel haben und nicht fliegen).

Schlussfolgerungen des intelligenten Agenten

Unser intelligenter Agent konnte beim Schlussfolgern drei Strategien verfolgen, die auf verschiedenen mathematischen Systemen, deren Bezeichnungen historisch gewachsen sind, basieren:

• Beim System P wird über die Menge aller für die Wissensbasis R zulässigen Rankings geschlussfolgert. Es zieht daher seine Schlüsse sehr vorsichtig.
• Beim System Z wird der Rang eines Szenarios lediglich durch den Wert der höchsten exzeptionellen Regel beeinflusst, die durch dieses Szenario verletzt wird. Es lässt keine Vererbung der Eigenschaften einer Oberklasse bei Unterklassen zu, die Ausnahmeeigenschaften aufweisen.
• Bei den allgemeinen C-Repräsentationen wird der Rang eines Szenarios durch alle verletzten Regeln beeinflusst. Die minimalen C-Repräsentationen liefern hingegen die minimalen Implausibilitätsgrade der Szenarien, wobei drei unterschiedliche Minimalitätsmaße (cw, sum, ind) existieren. Ferner kann man entweder skeptisch, leichtskeptisch oder leichtgläubig schlussfolgern.

Hierzu ein Anwendungsbeispiel: Malaria tropica ist eine weitverbreitete und lebensbedrohliche Krankheit in Afrika südlich der Sahara. Sie wird durch eine Infektion mit einem einzelligen Parasiten, Plasmodium falciparum, verursacht. Der Malariaerreger wird durch Anopheles Mücken übertragen. Aber nicht jeder mit P. falciparum infizierte Mensch erkrankt an Malaria: Einige Menschen besitzen eine erbliche Form des Hämoglobingens – das sog. Sichelzellengen. Zwei Kopien des defekten Gens verursachen eine Verformung der roten Blutkörperchen und eine schwere Anämie, während eine Kopie die Funktion dieser sauerstoff-transportierenden Zellen nicht beeinträchtigt. Auffallend ist, dass in Malariagebieten das Sichelzellengen relativ häufig ist. Träger von nur einer Kopie haben dort einen Vorteil gegenüber denen ohne Sichelzellengen, da letztere eher an Malaria sterben. In Afrika gibt es beispielsweise Gegenden, in denen fast ein Drittel der Bevölkerung ein verändertes Hämoglobingen aufweist. Die beiden wichtigsten Präventionsstrategien, um eine Malariaerkrankung zu vermeiden, sind die Vermeidung von Mückenstichen und die Abtötung von bereits eingedrungenen Malariaparasiten (Chemoprophylaxe). Da sich der Malariaerreger genetisch ständig wandelt, ist immer mit der Entwicklung von Resistenzen gegen die gängigen Medikamente zu rechnen.

Um den Ausgang einer Malariaerkrankung bei einem infizierten Patienten h zu modellieren, haben wir die Signatur Σ = {h, m, s, p, r} mit nachfolgender Semantik verwendet. Die Variable h steht für die mit dem Malariaerreger infizierten Patienten. Die Variable m ist wahr, wenn der infizierte Patient schwer an Malaria erkrankt. Die Variable s drückt aus, dass der Patient eine Kopie des Sichelzellengens in sich trägt. Eine angewandte Chemoprophylaxe wird mit einem p und eine Infektion mit einem dagegen resistenten Pathogen mit einem r modelliert. Die Wissensbasis KB_malaria enthielt:

• (¬s| h) Die infizierten Patienten haben normalerweise kein Sichelzellengen.
• (m|¬s) Ein fehlendes Sichelzellengen erlaubt es normalerweise, schwer an Malaria zu erkranken.
• (¬m|s) Ein Sichelzellengen erlaubt es normalerweise nicht, schwer an Malaria zu erkranken.
• (¬m|p) Die Anwendung einer Chemoprophylaxe erlaubt es normalerweise nicht, schwer an Malaria zu erkranken.
• (m|pr) Die Anwendung einer Chemoprophylaxe und das Vorliegen einer Resistenz dagegen erlauben es normalerweise, schwer an Malaria zu erkranken.

Wir haben die Wissensbasis bzw. unseren Agenten u. a. mit folgenden Fragen konfrontiert:

• (m|h) Erkranken die mit dem Malariaerreger infizierten Patienten normalerweise schwer an Malaria?
• (m|hpr) Erkrankt ein Patient, der eine Malariaprophylaxe anwendet und beim Malariaerreger eine Resistenz gegen diese Prophylaxe vorliegt, normalerweise schwer an Malaria?
• (m|hprs) Erkrankt ein Patient, der ein Sichelzellengen aufweist, bei der Anwendung einer Malariaprophylaxe und dem Vorliegen einer Resistenz dagegen, normalerweise schwer an Malaria?

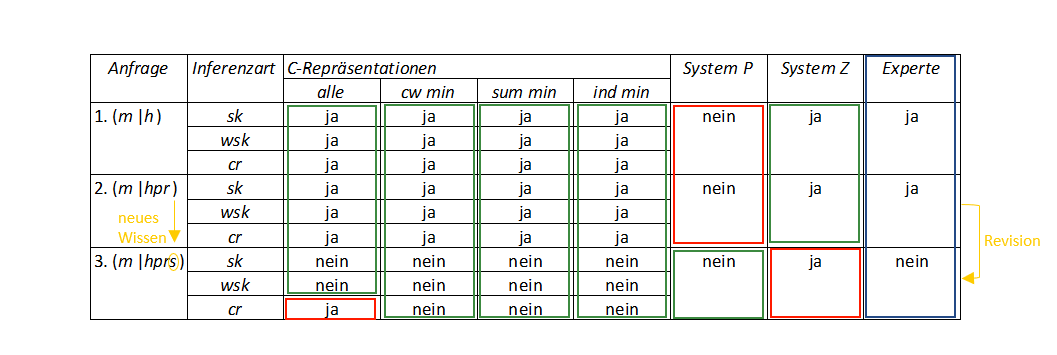
Die erste Frage soll vom KI-Agenten mit einem „Ja“ beantwortet werden, da die infizierten Menschen normalerweise kein Sichelzellengen tragen und daher schwer an Malaria erkranken. Die zweite Frage soll ebenfalls mit einem „Ja“ beantwortet werden. Die letzte Frage ist am interessantesten, da hier zwischen zwei widersprüchlichen Argumenten der Wissensbasis abgewogen werden muss: Einerseits erkranken infizierte Menschen schwer an Malaria, wenn sie eine Chemoprophylaxe anwenden und beim Malariaerreger dagegen eine Resistenz besteht. Andererseits schützt ein Sichelzellengen gegen einen schweren Verlauf der Krankheit. Empirisch wiegt das zweite Argument schwerer, da ein Sichelzellengen auch gegen Prophylaxe-resistente Malariaerreger schützt. Der Vergleich zwischen der zweiten und dritten Frage zeigt, dass einzelne Systeme des Agenten revidierbares Schließen ermöglichen: Addieren wir s zu unserer Anfrage, so können wir m nicht mehr ableiten.

Fazit

Wir konnten zeigen, wie biomedizinisches Wissen mithilfe der qualitativen konditionalen Logik ausgedrückt werden kann. Hierbei stellten wir fest, dass vor allem beim skeptischen und leichtskeptischen Schlussfolgern mittels C-Repräsentationen die Antworten des intelligenten Agenten mit den Antworten eines menschlichen Experten übereinstimmten und damit revidierbares Schließen auch für Maschinen möglich ist. Da die zugrundeliegenden Algorithmen zunächst zu optimieren sind, wird sich das Potential dieses KI-Ansatzes erst zukünftig zeigen. Wenn genügend große Wissensbasen algorithmisch verarbeitet werden können, ist davon auszugehen, dass ein solcher KI-Agent auch menschliche Experten sinnvoll unterstützen kann.

Systeme auf Basis qualitativer Konditionale ermöglichen die Revision von Schlussfolgerungen bei sich ändernden Wissensständen, was insbesondere im medizinischen Bereich von großer Bedeutung ist. Im Gegensatz zu den wahrscheinlichkeitsbehafteten Ergebnissen einer quantitativen Modellierung erhält der Anwender hier eine eindeutige Ja- bzw. Nein-Antwort auf seine Frage. Anders als bei neuronalen Netzwerken kann das Schlussfolgern eines solchen Systems zudem leichter transparent gemacht werden, da sich durch die regelbasierte Modellbildung seine Funktionsweise gut nachvollziehen lässt.

---

Literatur

1) J. Haldimann, A. Osiak, C. Beierle. Modelling and Reasoning in Biomedical Applications with Qualitative Conditional Logic. 10.1007/978-3-030-58285-2_24. (2020)

2) D. Kahneman. Thinking, fast and slow. New York: Farrar, Straus and Giroux. (2011) 3) J. Pearl, D. Mackenzie. The Book of Why: The New Science of Cause. Basic Books (2018)

3) J. Pearl, D. Mackenzie. The Book of Why: The New Science of Cause. Basic Books (2018)

Dieser Beitrag wurde verfasst von: